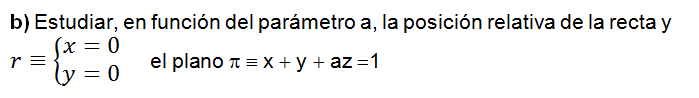Ejercicios resueltos de geometría en el espacio de pruebas de acceso PAU selectividad de diferentes comunidades autónomas
Ejercicio resuelto clásico de examen
Ver solución

Problema TENDENCIA EN EXÁMENES
Un depósito en forma de paralelepípedo, de base cuadrada ABCD, apoya completamente su base sobre una rampa en un local, quedando una arista superior pegada al techo. Se considera un sistema de ejes, con los semiejes positivos en un rincón del local. La arista inferior paralela a la que se apoya en el techo y no en su misma cara, tiene vértices de coordenadas A(1,1,1,1) B(1,3,1) La ecuación del plano que contiene a la rampa es : 4x-3z=1 1 y el vértice sobre el punto A es A´(1,1,6) se pide:
a) (0.5 puntos) Calcular una ecuación del plano que contiene a las aristas AB y AA′ .
b) (1 punto) Calcular los otros dos vértices, C y D, de la base.
c) (1 punto) Calcular el volumen del depósito.
VER SOLUCIÓN
Pau Madrid Junio 2015 4A
Ver solución apartado a

Pau Madrid Junio 2015 1B
b)Determinar la distancia de P a r
c)Existe algún punto R de la recta r, de modo que los puntos O, P y R estén alineados? En caso afirmativo, encontrar el punto (o los puntos) con esa propiedad o, en caso negativo, justificar la no existencia.
Pau Castilla y león Junio 2015 2A
a)Calcular la recta que corta perpendicularmente al eje OZ y que pasa por el punto P =
(1, 2,3)
ver solución
Pau Castilla y león Junio 2015 2B
Pau Andalucía Junio 2015 4a
Sean los puntos A(0,1,1), B(2,1,3), C(-1,2,0) y D(2,1,m).
(a) [0’75 puntos] Calcula m para que A, B, C y D estén en el mismo plano.
Ver solución(b) [0’75 puntos] Determina la ecuación del plano respecto del cual A y B son simétricos.
Ver solución (c) [1 punto] Calcula el área del triángulo de vértices A, B y C.
Ver soluciónPau Andalucía Junio 2015 4B
Sea el plano π ≡ 2x + y – z + 8 = 0.
(a) [1’5 puntos] Calcula el punto P’, simétrico del punto P(2,-1,5) respecto del plano π. Ver solución

Ver parte 1 ver parte 2
Ejercicio Madrid Junio 2013 selectividad

Ejercicio resuelto Selectividad Islas baleares Junio 2013
Determínese el punto simétrico de P(1,1,1) respecto al plano π: x-y+z=5
Ejercicio Selectividad Andalucía junio 2013
Se consideran los puntos P(2,3,1) y Q( 0,1,1)
Halla la ecuación del plano π respecto del cual P y Q son simétricos
Para seguir al profesor10demates , recibir todas las novedades y consultarle dudas podéis SUSCRIBIROS y retwiterame en las siguientes redes sociales: