Distribución Normal Estándar N(0,1)
Explicación de la tabla
Distribución normal ejemplos resueltos
Intervalos
Intervalos simétricos
Cuidado que el siguiente ejercicio tiene » trampa»
Distribución normal gráficamente
Distribución normal «al revés»
Calcular K
Caso Intervalo simétrico
TIPIFICAR DISTRIBUCION NORMAL
Tipificación N(μ,σ)
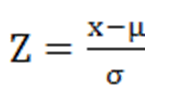
Siendo X lo que me preguntan μ la media σ la desviación típica recordar que σ2 es la varianza , luego la desviación típica es la raíz cuadrada de la varianza:
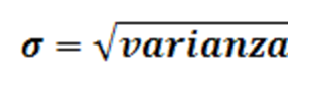
EJERCICIOS DE DISTRIBUCION NORMAL RESUELTOS
1 Calcula en una N(20, 4) las siguientes probabilidades: parte 1 parte2
a) P(X ≤ 23)
b) P(X ≥ 16)
c) P(23 ≤ X ≤27)
d)P(15 ≤ X ≤ 22)
e)P(15 ≤ X ≤ 18)
Vamos a realizar 3 ejercicios que son clásicos de examen y aprovecharemos para trabajar las claves , ciertos conceptos trucos y claves y así dominaremos el tema ver vídeo
Ejercicio resuelto clásico de examen 01
La temperatura del cuerpo humano sigue una distribución normal de media 37ºC y desviación típica 0,5ºC.
a) Calcular la probabilidad de que la temperatura de una persona sea menor que 36,5ºC
b) Calcular la probabilidad de que la temperatura de una persona sea mayor que 36ºC
c) Calcular la probabilidad de que la temperatura de una persona esté comprendida entre 36ºC y 38ºC
Ejercicio resuelto clásico de examen 02
Las notas de Matemáticas II de 500 alumnos presentados al examen de EBAU tienen una distribución normal con media 6,5 y varianza 4.
a) Calcule la probabilidad de que un alumno haya obtenido más de 8 puntos.
b) ¿Cuántos alumnos obtuvieron notas menores de 4 puntos?
Ejercicio resuelto clásico de examen 03
En un instituto la altura media es de 1,78 m con una desviavión típica de 20 cm . Si elegimos un alumno al azar calcula la probabilidad de :
a) Mida más de 1,85 m
b) Mida menos de 1,7 m
c) Mida entre 1,75 m y 1,9 m
Ejercicios clásicos de examen nivel full
En los últimos años este tipo de ejercicios se han convertido en súper clásicos de examen , así que vamos a meterle caña , ya sabes si en clase pronto tenéis examen compártelo en los grupos de clases VAMOS A POR NOTAZA !!!
Ejercicio clásico de examen Full
El tiempo empleado, en minutos, para obtener la respuesta de un test para detectar cierta enfermedad sigue una distribución normal de media 20 y de desviación típica 4.
a) ¿En qué porcentaje de test se obtiene el resultado entre 16 y 26 minutos?
b) ¿Cuántos minutos son necesarios para garantizar que se ha obtenido la respuesta del 96.41% de los test?
c) ¿Cuántos minutos son necesarios para garantizar que se ha obtenido la respuesta del 37,45% de los test?
Ejercicio clásico de examen calcular nota de corte
Las notas que se han obtenido por 1000 opositores han seguido una distribución normal de media 4,05 y desviación típica 2,5. a) ¿Cuántos opositores han superado el 5?
b) Si tenemos que adjudicar 330 plazas, calcula razonadamente la nota de corte.
Ejercicio clásico de examen como calcular la media de una distribución normal
La velocidad de los vehículos en una autopista con límite de velocidad de 120 km/h sigue una distribución normal de media µ km/h y desviación típica s =10 km/h. Se sabe que el 69,15% de los vehículos no sobrepasan la velocidad de 130 km/h
a) Calcule la media de esta distribución.
b)¿Cuál es el porcentaje de vehículos que no sobrepasan la velocidad máxima permitida?
c) La DGT establece una multa de 100 euros a los vehículos que viajan entre 120 y 150 km/h ¿Cuál es la probabilidad de ser sancionado con dicha multa?
Ejercicio clásico de examen como calcular la desviación típica de una distribución normal
Una empresa ha llevado a cabo un proceso de selección de personal. Las puntuaciones obtenidas por los aspirantes en el proceso de selección siguen una distribución normal, X, de media 5.6 y desviación típica σ. Sabiendo que la probabilidad de obtener una puntuación X ≤ 8.2 es 0.67, calcule σ.
a) Más de 4 Kg
b) menos de 3,5 Kg
c) Más de 3 Kg
d) Menos de 2,5 Kg
Ejercicio El número de libros prestados semanalmente en la biblioteca de un centro escolar sigue una distribución
normal de media 20 y desviación típica 2,5. Calcula la probabilidad de que en
una semana se presten entre 15 y 25 libros.
Ejercicio Carolina Rodríguez fué bautizada hace muchos años como la ‘gimnasta milagro’. Ha sido olímpica en Atenas 2004 , Londres 2012 y Río 2016 , donde ha sido octava ( Diploma Olímpico ) En los juegos de Río se convirtió en la gimnasta rítmica más longeva en disputar una final , con 30 años de edad . Si la media de su puntuación en el ejercicio de pelota es de 17,65 con una desviación típica de 0,20 Calcular la probabilidad de que obtenga entre 17,5 y 18 en un ejercicio. Ver solución
Prueba de acceso mayores de 25 años universidad CAD Matemáticas aplicadas a las ciencias sociales
La vida útil de un modelo de pila sigue una ley Normal con una media de 100 horas y desviación típica de 10 horas:
a)¿Qué porcentaje de este modelo de pila tendrá una duración inferior a 120 horas?
b) Halle la probabilidad de que una pila de este modelo elegida al azar, tenga una duración comprendida entre 90 y 110 horas.
Prueba de acceso mayores de 25 años universidad CAD Matemáticas aplicadas a las ciencias sociales
El peso de unas manzanas de una huerta sigue una ley Normal con una media de 150 gramos y desviación típica de 20 gramos:
a)¿Qué porcentaje de estas manzanas tendrá un peso inferior a 115 gramos?
b) Halle la probabilidad de que una manzana de este huerto elegida al azar, tenga un peso comprendido entre 165 y 220 gramos
OTRAS ENTRADAS QUE TE PUEDEN INTERESARCURSO DE MATEMÁTICAS 3º ESOCURSO DE FÍSICA Y QUÍMICA 3º ESO
CURSO DE FÍSICA Y QUÍMICA 4º ESO
CURSO DE MATEMÁTICAS 1º BACHILLERATO
CURSO DE MATEMÁTICAS SOCIALES 1º BACHILLERATO
CURSO DE FÍSICA Y QUÍMICA 1º BACHILLERATO
CURSO MATEMÁTICAS 2 BACHILLERATO








15 comentarios
De lujo! Todo entendido, ahora a practicar para no olvidar. Gracias Sergio.
De lujo! Todo entendido, ahora a practicar. Gracias Sergio!
Facil, facil, facil, gracias
ha sido facil entenderlo y asimilarlo, gracias mil,gracias Sergio
tal como tu lo explicas es muy sencillo entenderlo, gracias!!!
Muy fácil nos lo pones. Donde están las tablas? Dices en el video que están el blog pero no las encuentro
Esta semana la subo
muy buenos los videos….
profe puede hacer un ejemplo de intervalos entre un valor negativo y un valor positivo usando la campana de gauss.. por favor… le lo agradeciria bastante
GRACIAS
Hola Sergio! en la parte 3 de distribución normal gráfica no aparece el video que le corresponde! has vuelto a subir la parte 2.
Gracias por este maravilloso blog! Estela
Gracias lo corregiré
Hola Sergio!! Muchísimas gracias por tus videos 🙂 Sólo comentarte que, en "Distribución normal al revés", los videos con los enlaces a las soluciones de "Ejercicio" y "Caso intervalo simétrico" están cruzados: al pinchar en "ver solución" de "Ejercicio" me sale la solución de "caso intervalo simétrico" y viceversa. Un abrazo!!
gracias lo apunto para cambiarlo
Estoy enganchadísima a tus vídeos. Eres genial
Se entiende todo genial. Para mí eres el mejor muchas gracias por tu gran trabajo haces que todo sea muy fácil.
Saludos
Muchas gracias Silvia