Cómo hallar el DOMINIO de una función
Aprenderemos a calcular el domino de diferentes tipos de funciones ( polinómicas , racionales Iracionales con raices pares e impares , logaritmicas , exponenciales seno y coseno ) para lo que realizaremos un Súper resumen , ejemplos y ejercicios resueltos
Dominio de una función
👉 Ver vídeo Introducción y por qué son tan importantes los dominios
Es un concepto muy importante , ya que va a ser lo primero que hagamos cuando trabajemos con funciones , si lo calculamos mal , ¡ la hemos liado parda! Pero no te preocupes vamos a hacer un súper resumen con múltiples ejemplos en vídeo , cuando lo acabes serás una maquina del cálculo de dominios de funciones y ninguno se te resistirá.
¿Qué es el dominio de una función?
Llamamos dominio de una función al conjunto de valores de x para los que existe una función ¿Cuáles son los valores de x para los que la función no existe? Son aquellos valores que nos dan operaciones que no se pueden realizar ( dividir entre cero , raíces pares de números negativos , etc.. ) En los siguientes apartados los veremos paso a paso.
Lo denominaremos como Dom f(x)
¿Cómo se calcula el dominio de una función?
Deberemos calcular los valores de x donde exista la función, esto depende del tipo de función con la que trabajemos , vamos a aprender el procedimiento y realizar varios ejemplos para calcular el dominio de cada tipo de función.
Resumen y ejercicios resueltos de dominio de funciones
Dominio de una función polinómica
Ver Vídeo Dominio de un polinomio
La función existe para cualquier valor de x , luego su dominio será todos los números reales
Dom f(x) = R
Ejercicio resuelto
Calcula el dominio de f(x) = x3-6x2+2x-4
Dominio de una función racional (cociente de polinomios)
Ver vídeo Dominio de una función RACIONAL
f(x)=P(X)/Q(X)
No podemos dividir entre cero, luego la función existe para todos los valores menos para las x que hacen cero el denominador ( resolvemos la ecuación Q(x)=0 para obtener los puntos de no dominio )
Dom f(x) = R- { Q(x)=0 }
Ejercicio resuelto
Calcula el dominio de las siguientes funciones racionales:
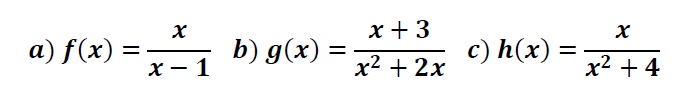
Dominio de una función Irracional con raíces pares
Ver Vídeo Dominio de una función IRRACIONAL PAR
![]()
siendo n un número par y u el radicando ( recuerda que el radicando es lo que está dentro de la raíz)
No existen raíces pares de números negativos , luego el dominio serán los valores de x , que hagan que u≥0 ( “ resolvemos la inecuación radicando mayor o igual que cero “)
Dom f(x) → u≥0 ,podemos expresarlo mejor cómo Dom f(x)={ x ϵ R / u≥0 }
Ejercicio resuelto
Calcula el dominio de las siguientes funciones Irracionales con raíces de índice par
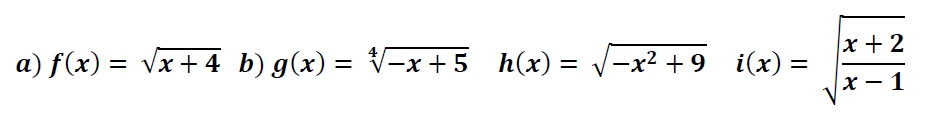
Si los videos te han servido , dale al LIKE y SUSCRIBETE 🚂 http://goo.gl/CMFnu0 y activa la campanilla🔥, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
Dominio de una función logarítmica
Ver vídeo Dominio de un LOGARITMO
f(x)=logu
No existe el logaritmo de cero ni de números negativos, luego el dominio serán los valores de x , que hagan que u>0 ( “ resolvemos la inecuación lo de dentro del logaritmo mayor que cero “)
TRUCO son iguales a los dominios de raíces de índice par , con la diferencia que no existe el logaritmo de cero ( la raíz de cero es cero ), luego en este caso todos los intervalos serán abiertos
Dom f(x) → u>0 podemos expresarlo mejor cómo Dom f(x)={ x ϵ R / u>0 }
Ejercicio resuelto
Calcula el dominio de las siguientes funciones logarítmicas
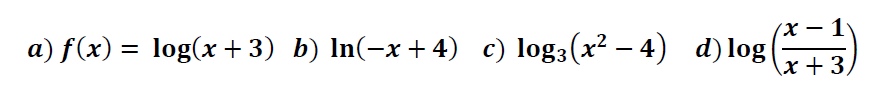
Dominio de una función Irracional con raíces impares
Ver vídeo Dominio de una función IRRACIONAL IMPAR
![]()
siendo n un número impar y u el radicando (recuerda que el radicando es lo que está dentro de la raíz)
Existen raíces de índice impar de cualquier número real , luego el dominio f(x) será igual al dominio del radicando
Dom f(x)= Dom u
Ejercicio resuelto
Calcula el dominio de las siguientes funciones Irracionales con raíces de índice Impar
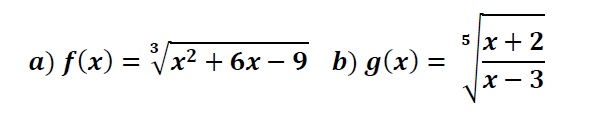
Dominio de una función exponencial
Ver vídeo Dominio de una EXPONENCIAL
f(x)=au
Como existen potencias de un número de cualquier número real , no influyen en el dominio luego el dominio f(x) será igual al dominio del exponente
Dom f(x)= Dom u
Ejercicio resuelto
Calcula el dominio de las siguientes funciones exponenciales
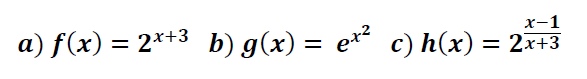
Dominio de una función trigonométrica: Seno y coseno
Ver vídeo Dominio de una trigonométrica SENO COSENO
f(x)= sen(u) f(x)= cos(u)
Como existen senos y cosenos de cualquier número real , no influyen en el dominio luego el dominio f(x) será igual al dominio de lo de dentro del seno o del coseno
Dom f(x)= Dom u
Ejercicio resuelto
Calcula el dominio de las siguientes funciones trigonométricas:
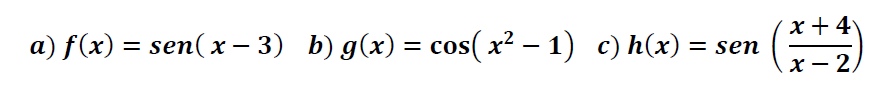
Cuadro resumen Dominio de Funciones

Ejercicios resueltos de exámenes
Calcula el dominio de las siguientes funciones
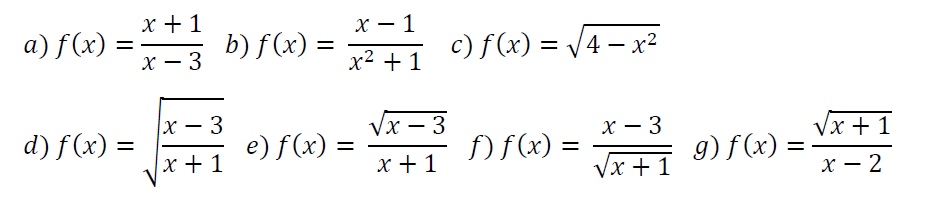
Dominio y recorrido de una función a partir de su gráfica
Dominio y recorrido a partir de la gráfica
OTRAS ENTRADAS QUE TE PUEDEN INTERESAR
CURSO DE MATEMÁTICAS 1º BACHILLERATO
CURSO DE MATEMÁTICAS SOCIALES 1º BACHILLERATO
CURSO DE FÍSICA Y QUÍMICA 1º BACHILLERATO
CURSO MATEMÁTICAS 2 BACHILLERATO
UNIVERSIDAD MATEMÁTICAS FÍSICA Y QUÍMICA








