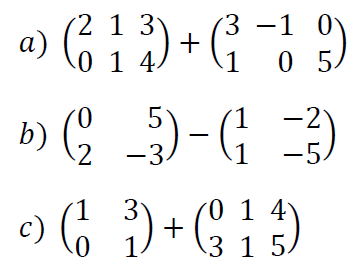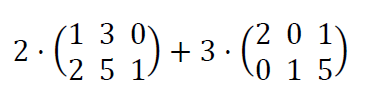Operaciones con Matrices

Explicaciones y ejemplos resueltos paso a paso de operaciones con matrices : suma , resta , multiplicación por un escalar

Suma y resta de matrices

Para sumar y restar matrices las matrices tienen que tener las mismas dimensiones, (es muy intuitivo)

Suma y resta de matrices ejercicios resueltos

Opera ver solución

Propiedades suma de matrices

La suma de dos matrices de dimensión m x n es otra matriz de orden m x n.

Propiedad Conmutativa:

A + B = B + A

Propiedad asociativa:

A + (B + C) = (A + B) + C

Matriz neutra:

El elemento neutro es una matriz en la que todos sus elementos son cero ( matriz nula) y tiene las mismas dimensiones que A

A + 0 = A

Matriz opuesta:

La matriz opuesta es aquella en que todos los términos son iguales a los de A , pero cambiados de signo

A + (−A) = O

Producto de un número (escalar) por una matriz

Multiplicamos todos los elementos de la matriz por el número

Ejemplo

Opera ver solución

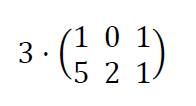
Ahora te dejo un ejemplo para que practiques , si lo haces bien ponte un MB bien grande y dímelo en los comentarios del vídeo.

Ejemplo producto de un escalar por una matriz

Opera ver solución

Despúes de ver la suma y la multiplicación por un escalar vamos a ver , los sistemas de ecuaciones matriciales , la multiplicación , ten paciencia no es difícil pero si liosa y también la potencia , con un par de ejercicios clásicos de exámenes .

Sigue los siguientes enlaces 👇👇👇👇👇👇👇

Sistemas de ecuaciones matriciales