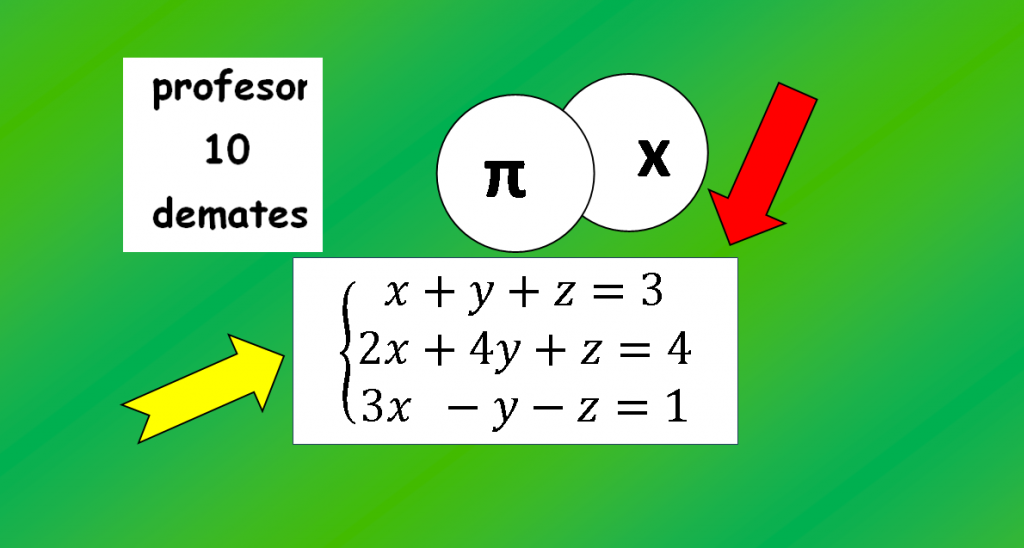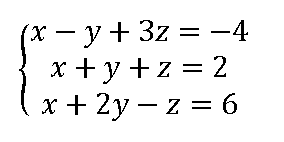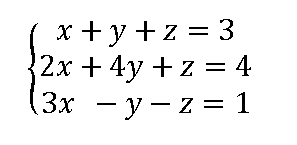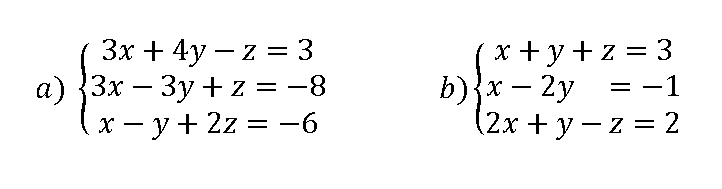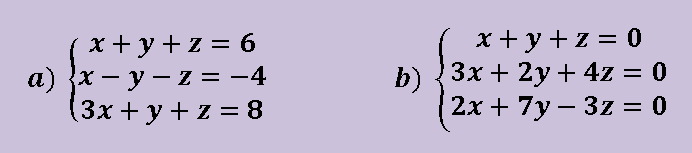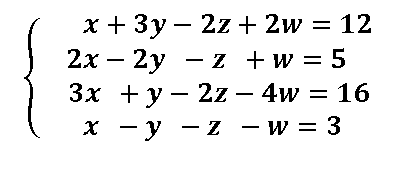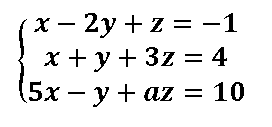Método de Gauss Ejercicios Resueltos paso a paso , sistemas de ecuaciones lineales 3×3 , 4×4 explicación de ejemplos desde cero . aprenderemos a clasificar y a resolver Sistemas Compatibles Determinados SCD , Sistemas Compatibles Indeterminados SCI y Sistemas Incompatibles SI
Método de Gauss Sistemas de ecuaciones
Para resolver sistemas de ecuaciones por el método de Gauss , seguiremos los siguientes pasos
Paso 1 (lo veremos explicado detalladamente en los vídeos), obtenemos un sistema equivalente escalonado reducido
Paso 2 (lo veremos explicado detalladamente en los vídeos)
Una vez obtenido el sistema escalonado iremos de abajo a arriba obteniendo las soluciones
Método de Gauss sistemas de ecuaciones 3×3
Ejercicio resuelto 01 Resuelve el siguiente sistema de ecuaciones
Ejercicio resuelto 02 ver solución
Resuelve los siguientes sistemas de ecuaciones
Ahora te toca practicar , resuelve los siguientes sistemas y abre el vídeo para corregirlos , muy importante aprende de los errores y si los haces bien ponte un MB 😉
Ejercicio resuelto 03
Resuelve los siguientes sistemas de ecuaciones
Apartado a) ver solución Apartado b) parte 1 parte 2
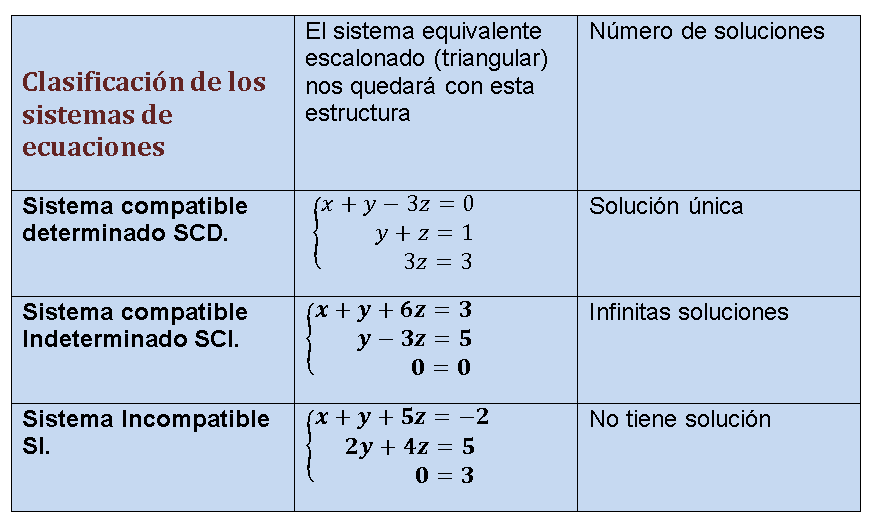
Clasificación de los sistemas de ecuaciones
La clasificación de sistemas de ecuaciones y su resolución va a ser muy importante a partir de ahora en nuestra “vida matemática” Así que vamos a meterle caña para transformarnos en máquinas .Siempre vamos a tener que clasificar el sistema y luego resolverlo.
IMPORTANTE VER EXPLICACIÒN
Clasificación de los sistemas de ecuaciones Dependiendo del número de soluciones
Sistemas compatibles determinados SCD.
Tienen una única solución.
El sistema equivalente escalonado (triangular) nos quedará con esta estructura
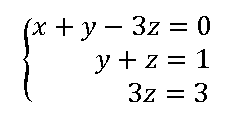
Sistemas compatibles Indeterminados SCI.
Tienen infinitas soluciones
El sistema equivalente escalonado (triangular) nos quedará con esta estructura
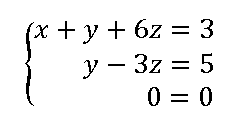
Sistemas Incompatibles SI.
No tienen solución
El sistema equivalente escalonado (triangular) nos quedará con esta estructura
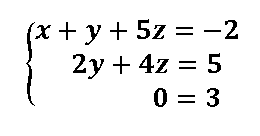
También podemos clasificar los sistemas en :
a) Homogéneos . Son sistemas de ecuaciones lineales donde TODOS sus términos independientes son 0
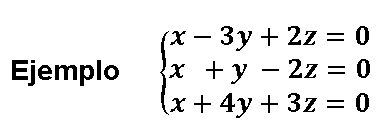
Los sistemas Homogéneos, tienen dos propiedades muy interesantes
1) El sistema siempre es Compatible (Determinado o Indeterminado)
2) Si el sistema es compatible determinado, tiene la solución trivial, que es aquella en las que todas sus soluciones son cero : x=0 , y=0 , z=0
b) Heterogéneos Cuando No son homogéneos
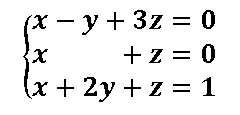
Ejercicios resueltos Sitemas Compatibles Indeterminados
Clasifica y resuelve los siguientres sistemas de ecuaciones por el método de Gauss
Ver solución apartado a ver solución apartado b
Ejercicios resueltos Sitemas Incompatibles
Clasifica y resuelve los siguientres sistemas de ecuaciones por el método de Gauss ver solución
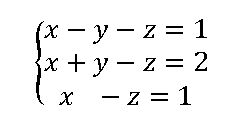
Ejercicios para practicar Ahora te toca a ti 😉 clasifica y resuelve los siguientes sistemas y comprueba la solución con los vídeos
Apartado a parte 1 parte 2 Apartado b parte 1 parte 2
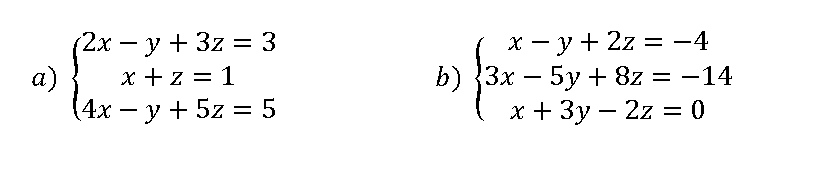
lo genial del método de Gauss es que es aplicable a sistemas con cualquier número de incógnitas , para verificarlo vamos a resolver un sistem de 4 ecuaciones con 4 incógnitas
Sistemas de 4 ecuaciones con 4 incógnitas
Igual que es los sistemas de ecuaciones 3×3 , lo primero que tenemos que hacer es obtener , el sistema equivalente reducido escalonado y luego resolver el sistema.
Lo mejor es que veamos un ejemplo resuelto paso a paso
Ejercicio resuelto sistemas 4×4 método de Gauss
IMPORTANTE
Si estás realizando el curso cero , vuelve a él , porque la resolución de problemas por ahora no es intereante , ya los resolveremos más adelante .
Si no estás en el curso cero , vamos a divertirnos con los problemas 🙂
Problemas de sistemas de ecuaciones Método de Gauss
Problema resuelto 01 Ver solución
Un grupo de estudiantes financia su viaje de fin de curso con la venta de participaciones de lotería, por importe de 1, 2 y 5 euros. Han recaudado, en total, 600 euros y han vendido el doble de participaciones de 1 euro que de 5 euros. Si han vendido un total de 260 participaciones, calcula el número de participaciones que han vendido de cada importe.
Problema resuelto 02 Ver solución
En una sucursal de una agencia de viajes se vende un total de 60 billetes de avión con destino a Londres, París y Roma. Sabiendo que el número de billetes para París es el doble de los vendidos para los otros dos destinos conjuntamente y que para Roma se emiten dos billetes más que la mitad de los vendidos para Londres, ¿cuántos billetes se han vendido para cada uno de los destinos?
Problema resuelto 03 Ver solución
CLÁSICO de examen
En un comercio de bricolaje se venden listones de madera de tres longitudes 90 cm 1,5 m y 2,4 m cuyos precios respectivos son 4 euros , 6 euros y 10 euros . Un cliente ha comprado 19 listones , con una longitud total de 30 m , que le han costado 126 euros en total . Calcula el número de listones de cada tipo que ha comprado el cliente
Problema resuelto 04 Ver solución
Clásico de examen
En un examen de matemáticas que constaba de tres problemas,un alumno obtuvo una calificación total de 7,2 La puntuación del primer problema fue un 40% más que la del segundo , y la del tercero fue el doble de la suma de las puntuaciones del primero y del segundo ¿cuál fue la puntuación de cada problema?
Ejercicio clásico de examen 2022
Tres primos, Pablo, Alejandro y Alicia, se van a repartir un premio de 9450 euros de forma directamente proporcional a sus edades. La suma de las edades de Pablo y Alejandro excede en tres años al doble de la edad de Alicia. Además, la edad de los tres primos juntos es de 45 años. Sabiendo que en el reparto del premio Pablo recibe 420 euros más que Alicia, calcule las edades de los tres primos y el dinero que recibe cada uno por el premio.
Examen junio 2019 ver solución
Una estudiante pidió en la cafetería 3 bocadillos, 2 refrescos y 2 bolsas de patatas y pagó un total de 19 euros. Al mirar la cuenta comprobó que le habían cobrado un bocadillo y una bolsa de patatas de más. Reclamó y le devolvieron 4 euros. Para compensar el error, el vendedor le ofreció llevarse un bocadillo y un refresco por solo 3 euros, lo que suponía un descuento del 40% respecto a sus precios originales. ¿Cuáles eran los respectivos precios sin descuento de un bocadillo, de un refresco y de una bolsa de patatas?
Ejercicio resuelto con porcentajes clásico de examen
Un banco invirtió 2 millones de euros en tres empresas diferentes , A , B , C. Lo que invirtió en A era el doble de lo que invirtió en B , la rentabilidad de la operación ha sido del 10% . Las acciones de la empresa A han aumentado su valor un 10% , las de B un 30% y las de C han perdido un 10% de su valor ¿ qué cantidad invirtió en cada empresa?
Ejercicio resuelto selectividad EVAU 2023
Muchos estudiantes cometieron un error realizando este ejercicio en el examen de selectividad , pero no te preocupes si ves el vídeo , tu nunca lo cometerás 😉
En una obra , para transportar la tierra extraída para la construcción de los cimientos de un edificio , se usan tres tipos de camiones diferentes : A, B, C . Los camiones tipo A tienen una capacidad de 14 toneladas , los de tipo B , de 24 toneladas y los de tipo C de 28 toneladas . Habría que traer un camión más del tipo A para igualar al número de camiones restantes . El 10% de la capacidad de todos los camiones de tipo B supone un séptimo de la de los de mayor tonelaje . Hoy , realizando un único viaje cada camión a máxima capacidad , se han extraído de la obra 302 toneladas de tierra ¿ Cuanta tierra ha sido transportada hoy por los camiones de cada tipo?
METODO DE GAUSS problema resuelto con infinitas soluciones compatible indeterminado
Este tipo de ejercicio es también un CLÁSICO de EXAMEN ya que vamos a obtener un sistema compatible indeterminado y tendremos que obtener sus infitas soluciones
Una papelería vende bolígrafos, rotuladores y libretas. Una libreta cuesta el doble que un bolígrafo y un rotulador juntos, un bolígrafo cuesta la sexta parte que una libreta, y un rotulador cuesta el doble que un bolígrafo. a) Plantee un sistema de 3 ecuaciones con 3 incógnitas que represente los datos del ejercicio. b) Calcule todas las posibles soluciones del sistema. c) Sabiendo que una libreta cuesta 18 euros, calcule el precio de cada producto.
Problema resuelto selectividad 2023 con porcentajes clásico de examen
Una marca de vehículos ha vendido este mes coches de tres colores: blancos, negros y rojos. El 60 % de los coches blancos más el 50 % de los coches negros representan el 30 % de los coches vendidos. El 20 % de los coches blancos junto con el 60 % de los coches negros y el 60 % de los coches rojos representan la mitad de los coches vendidos. Se han vendido 100 coches negros más que blancos. Determina el número de coches vendidos de cada color.
Problema modelo cero selectividad 2024
La primera interpretación en EE.UU. de la octava sinfonía de Mahler tuvo lugar en Filadelfia en 1916 con la participación de una orquesta, dos coros con el mismo número de miembros, un tercer coro infantil y, además, ocho cantantes solistas invitados especialmente y que no pertenecían a ninguno de los coros. La décima parte del número total de intérpretes de los tres coros era menor en 15 unidades al de miembros de la orquesta. Los miembros de cada uno de los dos coros no infantiles superaban en 140 unidades a la suma de componentes del coro infantil y los de la orquesta. El número de miembros de la orquesta excedía en 21 unidades a la doceava parte del total de intérpretes. ¿Cuántos interpretes tenía la orquesta y cada uno de los coros? ¿Cuántos intérpretes había en total?
Problema que se hizo viral por las redes sociales Competencial muy interesante de cara a la PAU 2025
En los años 2022 y 2023, Carlitos Alcaraz ganó un total de 10 torneos de categorías Grand Slam, Masters 1000 y ATP 500, lo que le proporcionó un total de 10.000 puntos. El número de torneos ganados de categoría ATP 500 fue 1 más que la mitad de la suma del número de torneos ganados de las otras dos categorías. En la siguiente tabla se detallan los puntos conseguidos por cada torneo ganado en cada una de las categorías:
Grand Slam = 2.000 puntos Masters 1000 = 1.000 puntos ATP 500 = 500 puntos
Con esta información, calcule el número de torneos de cada una de las tres categorías ganados por Carlitos en los años 2022 y 2023.
Madrid 2024 mates II
Se tienen listones de madera de tres longitudes diferentes: largos, intermedios y cortos. Puestos uno tras otro, tanto con dos listones largos y cuatro intermedios como con tres intermedios y quince cortos se consigue la misma longitud total. Un listón largo supera en 17cm la medida de uno intermedio más uno corto. Y con nueve listones cortos hemos de añadir 7 cm para igualar la longitud de uno intermedio seguido por uno largo. Se pide calcular la longitud de cada tipo de listón
Muy interesante
Consejos y procedimiento para la resolución de problemas
Leer detenidamente el enunciado, recomiendo leerlo como mínimo dos veces, la primera vez de forma general y en la segunda empezar a extraer los datos elegir las incógnitas y sacar las ecuaciones
Elegir y escribir las incógnitas y plantear las ecuaciones
Primero tenemos que elegir siempre las incógnitas x,y,z
Luego leer el enunciado despacio e ir planteando las ecuaciones de una en una, sin mezclar datos de una ecuación con otra, yo suelo subrayar lo que representa cada ecuación
Una vez planteado el sistema de ecuaciones 3×3, que sin lugar a dudas es con mucho lo más complicado, intentamos simplificar las ecuaciones, y colocarlas para que quede lo más sencillo posible.
Y por último los resolvemos
Para trabajar este tipo de problemas os recomiendo que planteéis muchos problemas de sistemas de ecuaciones 3×3 ( yo recomiendo cada 3 que planteo y simplifico, resolver solo uno, así en menos tiempo podemos trabajar el planteamiento ) , así poco a poco nuestro cerebro se irá acostumbrando y empezaremos a realizarlos como máquinas.
Problemas resueltos de sistemas de ecuaciones 3×3
solución selectividad matemáticas sociales Castilla y León Junio 2012 1 A
1A- Una fábrica produce tres tipos de herramientas: A, B y C. En la fábrica trabajan tres obreros, durante 8 horas diarias cada uno, y un revisor para comprobar las herramientas durante 1 hora diaria. Para fabricar una herramienta de tipo A se emplean 2 horas de mano de obra y se necesitan 6 minutos de revisión, para la fabricación de una de tipo B se emplean 4 horas de mano de obra y 4 minutos de revisión y para una de tipo C se necesitan 1 hora de mano de obra y 4 minutos de revisión. Por limitaciones en la producción, se deben producir exactamente 12 herramientas al día. Calcula el número de herramientas de cada tipo que se elaboran cada día en la fábrica.
solución selectividad matemáticas sociales Castilla y León Junio 2012 1 A
solución selectividad matemáticas sociales Madrid Junio 2012
Un estadio de fútbol con capacidad para 72000 espectadores está lleno durante la celebración de un partido entre los equipos A y B. Unos espectadores son socios del equipo A, otros lo son del equipo B, y el resto no son socios de ninguno de los equipos que están jugando. A través de la venta de localidades sabemos lo siguiente:
(a) No hay espectadores que sean socios de ambos equipos simultáneamente.
(b) Por cada 13 socios de alguno de los dos equipos hay 3 espectadores que no son socios.
(c) Los socios del equipo B superan en 6500 a los socios del equipo A.
¿Cuántos socios de cada equipo hay en el estadio viendo el partido?
solución selectividad matemáticas sociales Castilla y León Junio 2011 1 B
1B- Un grupo de estudiantes financia su viaje de fin de curso con la venta de
participaciones de lotería, por importe de 1, 2 y 5 euros. Han recaudado, en total, 600 euros y han vendido el doble de participaciones de 1 euro que de 5 euros. Si han vendido un total de 260 participaciones, calcula el número de participaciones que han vendido de cada importe.
solución selectividad matemáticas sociales Castilla y León Junio 2011 1 B
solución selectividad matemáticas sociales Castilla y León Septiembre 2009 1 B
1B- Compramos tres regalos A, B y C para tres amigos. Sabemos que hemos pagado 117 euros por los tres regalos tras habernos hecho un descuento del 10% sobre el precio total. Además sabemos que el precio del regalo C es el doble que el del regalo A y que el regalo C es 20 euros más caro que el regalo B. ¿Cuánto hemos gastado en cada regalo?
solución selectividad matemáticas sociales Castilla y León Septiembre 2009 1 B
solución selectividad matemáticas sociales Castilla y León Junio 2007 1 A
1A- Julia, Clara y Miguel reparten hojas de propaganda. Clara reparte siempre el 20% del total, Miguel reparte 100 hojas más que Julia. Entre Clara y Julia reparten 850 hojas. Plantea un sistema de ecuaciones que permita saber cuántas hojas reparte cada uno. Sabiendo que la empresa paga 1 céntimo por cada hoja repartida, calcula el dinero que ha recibido cada uno de los tres.
solución selectividad matemáticas sociales Castilla y León Junio 2007 1 A
Sistemas de ecuaciones por el método de Gauss con parámetros
OTROS CURSOS GRATUITOS QUE TE PUEDEN INTERESAR
Matemáticas 1º bachillerato ciencias sociales
Matemáticas 1º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias aplicadas a las ciencias sociales
UNIVERDIDAD Matemáticas Física Química y Estadística
Otros TEMAS que os pueden interesar
Integrales indefinidas , métodos de integración
