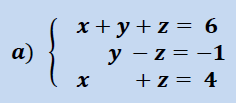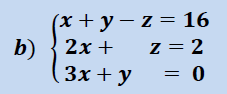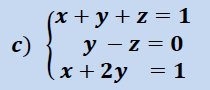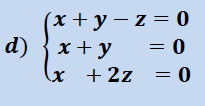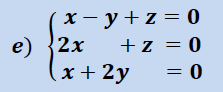Teorema de Rouché Frobenius Ejercicios resueltos , veremos la aplicación tan importante que tiene el teorema con ejemplos resueltos paso a paso , para ello primero tendremos que calcular el rango de las matriz de coeficientes y de la matriz ampliada . Matemáticas 2º bachillerato y universidad
Teorema de Rouché Frobenius
¿Qué dice el teorema de Rouche?
Enunciado Teorema de Rouché Frobenius
Utilizaremos este teorema para clasificar los sistemas de ecuaciones calculando el rango de la matriz de coeficientes rg(A) y el rango de la matriz ampliada rg(A*) , siendo n el número de incógnitas
¿Cómo aplicar el teorema de Rouche Frobenius?
Una vez clasificado el sistema de ecuaciones tendremos que resolverlo ,para ello nos vamos a apoyar en este cuadro. Ver vídeo explicativo
Ahora vamos a ver varios ejemplos donde aplicaremos el teorema de Rouché Frobenius para clasificar el sistema y luego una vez clasificado , lo resolveremos , siempre deberemos primero clasificar y luego resolver.
Recuerda que este teorema va a ser importantísimo en nuestra vida matemática así que vamos a dominarlo perfectamente con estos cinco ejemplos resueltos , después no habrá ejercicio que se nos resista
Vamos máquina !!!!!!!!!
Ejercicios Rouche Frobenius resueltos
Ejemplo Sistema Compatible Determinado (SCD)
Ejemplo Sistema Incompatible ( SI )
Sistema Compatible Indeterminado ( SCI )
Sistemas homogéneos Propiedades
Los sistemas Homogéneos son aquellos en que todos los términos independientes son cero (sino son homogéneos se les llama Hetereogéneos)
Los sistemas de ecuaciones homogéneos tienen varias propiedades interesantes que nos pueden ahorra bastante trabajo , por lo que vamos a verlas
En primer lugar siempre el rango de la matriz de coeficientes es igual al rango de la matriz ampliada
rg(A)=rg(A*)
Por lo que un sistema homogéneo Nunca puede ser incompatible , es decir siempre tienen solución.
En caso de que el Sistema homogéneo sea Compatible Determinado ( SCD) , decimos que tiene la solución trivial x=0 ; y=0 ; z=0
Sistema compatible Determinado Homogéneo ejercicio resuelto
Sistema compatible Indeterminado Homogéneo
OTRAS ENTRADAS QUE TE PUEDEN INTERESAR
Sistemas de ecuaciones con parámetros ejercicios y problemas resueltos
Método de Gauss Ejercicios Resueltos paso a paso