3.1 Diferencia de sucesos
$P(A∩\bar{B})=P(A)-P(A∩B)$
$P(\bar{A}∩B)=P(B)-P(A∩B)$
Ejercicios resueltos diferencia de sucesos
En un concurso la probabilidad de ganar un reloj es de 0,4 y de ganar un móvil 0,2 . La probabilidad de ganar los 2 regalos es de 0,05 . Calcular la probabilidad de ganar solo el móvil.
3.2 Diferencia simétrica
$P((\bar{A}∩B) U (A∩\bar{B}))=P(A)+P(B)-2P(A∩B)$
Ejemplo diferencia simétrica de sucesos ver vídeo
En un concurso la probabilidad de ganar un reloj es de 0,4 y de ganar un móvil 0,2 . La probabilidad de ganar los 2 regalos es de 0,05 . Calcular la probabilidad de ganar solo uno de los 2 regalos
3.3 Leyes de Morgan
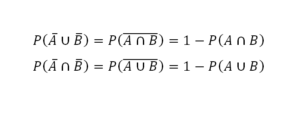
Ejercicios leyes de Morgan resueltos
En un concurso la probabilidad de ganar un reloj es de 0,4 y de ganar un móvil 0,2 . La probabilidad de ganar los 2 regalos es de 0,05 . Calcular la probabilidad de no ganar ningún regalo
ejercicios resueltos
En una ciudad, la probabilidad de que llueva un día de junio es del 10%, y de que haga sol un 75 %. Si no es posible que en un mismo día de junio llueva y haga sol simultáneamente, ¿cuál es la probabilidad de que en un día de junio no llueva ni haga sol?
ejercicios full de estambull
El 60% de los clientes de una frutería compran naranjas y el 30% no compra ni naranjas ni manzanas. ¿Qué porcentaje de clientes compra manzanas, pero no naranjas? Ver solución
PAU 2015 madrid matemáticas aplicadas a las ciencias sociales Ver solución

OTRAS ENTRADAS QUE TE PUEDEN INTERESAR
CURSO DE FÍSICA Y QUÍMICA 2 ESO
CURSO DE FÍSICA Y QUÍMICA 3º ESO
CURSO DE FÍSICA Y QUÍMICA 4º ESO
CURSO DE MATEMÁTICAS 1º BACHILLERATO
CURSO DE MATEMÁTICAS SOCIALES 1º BACHILLERATO
CURSO DE FÍSICA Y QUÍMICA 1º BACHILLERATO
CURSO MATEMÁTICAS 2 BACHILLERATO
UNIVERSIDAD MATEMÁTICAS FÍSICA Y QUÍMICA








4 comentarios
3.1 Diferencia de sucesos
P(A∩B¯)=P(A)−P(A∩B)
P(A¯∩B)=P(A)−P(A∩B)
Creo que deberías modificar la fórmula:
P(A¯∩B)=P(B)−P(A∩B)
gracias no me habia dado cuenta, la modifico
hola soy de mexico me estas ayudando mucho tus videos pero aun no puedo resolver este problema espero me puedan ayudar
1. Dados P(A)=0.4, P(B|A)= 0.3 y
P(B'|A')=0.2, determine:
a) P(A').
b) P(B|A').
c) P(B).
d) P(A intersección B).
e) P(A|B).
hola Sergio soy de México me han servido mucho tus videos pero aún no puedo resolver este problema
1. Dados P(A)=0.4, P(B|A)=0.3 y
P(B'|A')=0.2, determine:
a) P(A').
b) P(B|A').
c) P(B).
d) P(A intersección B).
e) P(A|B).