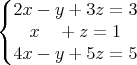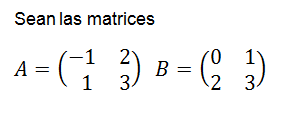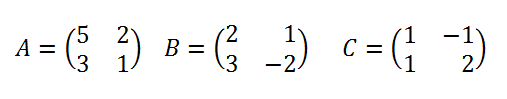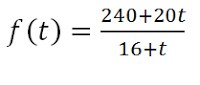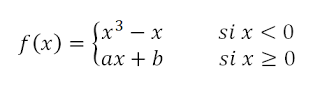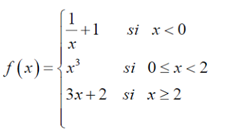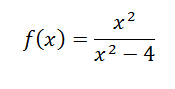Ejercicios y problemas resueltos de exámenes , matemáticas aplicadas a las ciencias sociales pdf , 2º bachillerato ,
Ejercicios y problemas resueltos de exámenes , matemáticas aplicadas a las ciencias sociales pdf , 2º bachillerato ,
Mas que un examen lo que vamos a realizar es un repaso para preparar el examen final de MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES de segundo de bachillerato , y también la selectividad . Si ves que flojeas en algún tema estudiarlo en el curso para aprobar MATEMATICAS APLICADAS A LAS CIENCIS SOCIALES de 2º de bachillerato .
Sistemas de ecuaciones
Discutir y resolver:
02 Un grupo de estudiantes financia su viaje de fin de curso con la venta de participaciones de lotería, por importe de 1, 2 y 5 euros. Han recaudado, en total, 600 euros y han vendido el doble de participaciones de 1 euro que de 5 euros. Si han vendido un total de 260 participaciones, calcula el número de participaciones que han vendido de cada importe.
Matrices
Ejercicio de Matrices 01
Ejercicio de Matrices 02
- a)Calcule las matrices X e Y se X+Y=2A y X+B=2Y ver solución
- b) Analice cuales de las siguientes operaciones con matrices se pueden realizar , indicando en los caso afirmativos las dimensiones de la matriz D ver solución
Ejercicio de Matrices 03
Determinantes
Ejercicio determinantes 01
- a) Estúdiese el rango de A según los valores del parámetro real k. ver solución
Ejercicio determinantes 02
Calcúlese, si existe, la matriz inversa de A para k = 3. Ver solución
Ejercicio determinantes 03 ver solución
Resolver la siguiente ecuación matricial A·X=B-C siendo
Sistemas de ecuaciones con parámetros
Estos ejercicios casi siempre caen en examen ( por no decir siempre ) llévalos perfectos tienen que ser puntos fijos en el examen
Recuerda que tienes que DOMINAR EL teorema de Rouché-Frobenius ( TE DEJO EL ENLACE POR SI LO NECESITAS)
09 Ejercicio ver solución
Discutir el siguiente sistema
Estoy preparando más ejercicios de sistemas de ecuaciones con parámetros
Puedes DISFRUTAR un rato con mi nuevo canal de experimentos
https://www.youtube.com/c/profesor10experimentos
PROGRAMACIÓN LINEAL
Ejercicio 01 programación Lineal EBAU EVAU
Un comercio dispone de 60 unidades de un producto A por el que obtiene un beneficio por cada unidad que vende de 250 €. También dispone de 70 unidades de otro producto B por el que obtiene un beneficio por unidad vendida de 300 €. El comercio puede vender como máximo 100 unidades de sus productos. Utilizando técnicas de programación lineal, determina las unidades de los productos A y B que el comercio debe vender para que su beneficio sea máximo y calcula dicho beneficio.
Ver inecuaciones , restricciones
Ejercicio 02 programación Lineal EBAU EVAU
En un taller textil se confeccionan 2 tipos de prendas: trajes y abrigos. Los trajes requieren 2 metros de lana y 1.25 metros de algodón y los abrigos requieren 1.5 metros de lana y 2.5 metros de algodón. Se disponen semanalmente de 300 metros de lana y de 350 metros de algodón, y esta semana deben fabricarse al menos 20 abrigos. Empleando técnicas de programación lineal, determina cuántos trajes y abrigos hay que hacer esta semana si se desea maximizar el beneficio obtenido, sabiendo que se ganan 250 euros por cada traje y 350 euros por cada abrigo. ¿A cuánto asciende dicho beneficio?
Ver inecuaciones , restricciones
FUNCIONES
Seguramente la parte más complicada , te dejo muchos ejercicios para que repases a full , los de continuidad , derivabilidad , con parámetros , y los de optimización donde me dan la función , son los más sencillos así que esos tipos tienes que llevarlos bien
Ejercicio resuelto funciones 01
Halla el valor de k para que la siguiente función sea continúa en todo R ver solución
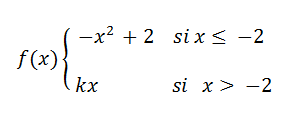
Ejercicio resuelto funciones 02
Se ha estimado que la población de un barrio de una gran ciudad evolucionará siguiendo el modelo
en miles de habitantes, donde t indica los años transcurridos desde su creación en 2005
- a) que población tenía el barrio en 2005?
- b) Que población tenía en 2015?
- c) A largo plazo la población se estabilizará? ver solución
Ejercicio resuelto funciones 03
Calcular el valor de los parámetros a y b para que la función definida a trozos f(x)sea derivable ver solución
Ejercicio resuelto funciones 04
Sea f(x)
. Ver solución
Ejercicio resuelto funciones 05
Calcular la ecuación de la recta tangente y normal de f(x)=x^2-3x+1 en x=-2
recta tangente y normal de una función en un punto 2
Ejercicio resuelto funciones 06.1
Se considera la función f(x)=-x3+bx2+x+d
- a) Calcular razonadamente los valores de b y d para que la función f(x) tenga un máximo relativo en el punto (1,4)
Ejercicio resuelto funciones 06.2
a)Calcular los parámetros a y b y = −2x2 + ax− b sabiendo que alcanza su máximo en el punto (2, 2) .
b)Calcula la ecuación de la recta tangente en el punto máximo.
Ahora vamos a ver problemas de optimización , los problemas en los que tenemos que sacar nosotros las funciones , problablemente sean los más dificiles , por eso os dejo varios que han caído en la EBAU , EVAU
Ejercicio resuelto funciones 07 Ver solución
El número de visitantes diarios a una feria de turismo viene dado por la función V(t)=-30(t2-14t-11) donde t ∈(0,10) es el tiempo (en horas) transcurrido desde la apertura de la feria.
- a) ¿Cuándo aumenta la afluencia de público y cuándo disminuye? ¿En qué momento se alcanza el número máximo de visitantes?
- b) Determina ese número máximo de visitantes.
Ejercicio resuelto funciones 08
Un estudio realizado por una empresa de producción de películas de acción prueba que el coste anual (en millones de euros) de contratación de los actores secundarios que utiliza en sus películas
sigue la función ,
donde x es el número de actores secundarios contratados. Calcula el número de actores secundarios contratados que hace mínimo el coste de contratación. ¿A qué cantidad asciende ese coste mínimo?ver solución
Ejercicio resuelto funciones 09
De entre todos los rectángulos de perímetro 8 calcular el que tiene área máxima. Ver solución
Ejercicio resuelto funciones 10 ver solución
Encuentra dos números positivos cuya suma sea 120 , tales que el producto de uno de ellos por el cuadrado del otro sea máximo
Ejercicio resuelto funciones 11 Un agricultor dispone de 3000 € para cercar un terreno rectangular, usando el río adyacente como lado con el fin de que el recinto sólo necesite 3 cercas. El coste de la cerca paralela al río es de 5 € por metro instalado, y el de la cerca para cada uno de los lados restantes es de 3 € por metro instalado. Calcula las dimensiones del terreno de área máxima que puede cercar con el presupuesto que tiene. Ver solución
Puedes DISFRUTAR un rato con mi nuevo canal de experimentos
https://www.youtube.com/c/profesor10experimentos
FUNCIONES Representación gráfica de funciones
Vamos a trabajar las funciones poolinómicas que son sencillas ( pero a veces caen ) y las racionales que son las funciones que más suelen caer . Te dejo el enlace al curso para ser una máquina de la representación gráfica de funciones por si lo necesitas .Curso de representación de funciones
Representación gráfica de funciones Función polinómica
Representar la siguiente función f(x)= x3+3x2
Ver Dominio,continuidad,simetría , puntos de corte y asíntotas
Ver monotonía y extremos relativos
Ver curvatura y puntos de inflexión
Representación gráfica de funciones Función Racional 01
Ver Dominio,continuidad,simetría , puntos de corte
Ver monotonía y extremos relativos
Ver curvatura y puntos de inflexión
Probabilidad
Suele caer siempre un ejercicio de diagrama de árbol y teorema de Bayes , teneis que trabajarlos duro porque tienen que ser puntos fijos en el examen
EJERCICIO PROBABILIDAD 01
En una bolsa hay cuatro bolas rojas y una verde. Se extraen de forma consecutiva y sin reemplazamiento dos bolas. Calcúlese la probabilidad de que:
- a) Las dos bolas sean del mismo color.
- b) La primera bola haya sido verde si la segunda bola extraída es roja.
EJERCICIO PROBABILIDAD 02
Un moderno edificio tiene dos ascensores para uso de los vecinos. El primero de los ascensores es usado el 45% de las ocasiones, mientras que el segundo es usado el resto de las ocasiones. El uso continuado de los ascensores provoca un 5% de fallos en el primero de los ascensores y un 8% en el segundo. Un día suena la alarma de uno de los ascensores porque ha fallado. Calcula la probabilidad de que haya sido el primero de los ascensores.
EJERCICIO PROBABILIDAD 03
La lista electoral de un determinado partido político está formada por un número igual de hombres y mujeres. Un análisis sociológico de dichas listas revela que el 60% de los hombres tienen 40 o más años de edad, mientras que el 30% de las mujeres tienen menos de 40 años. Se elige al azar una persona que forma parte de las listas electorales.
- a) Calcula la probabilidad de que tenga menos de 40 años.
- b) Sabiendo que tiene 40 o más años de edad, calcula la probabilidad de que sea mujer.
EJERCICIO PROBABILIDAD 04
En una ciudad, la probabilidad de que llueva un día de junio es del 10%, y de que haga sol un 75 %. Si no es posible que en un mismo día de junio llueva y haga sol simultáneamente, ¿cuál es la probabilidad de que en un día de junio no llueva ni haga sol? Ver solución
EJERCICIO PROBABILIDAD 05
Según el informe anual La Sociedad de la Información 2012, el 63% de los usuarios de móvil en España tiene un “Smartphone”. Entre los propietarios de este tipo de teléfono, el 77% lo emplea para su conexión habitual a internet. Sin embargo, entre los propietarios de otros tipos de teléfono móvil sólo el 8 % lo emplea para la conexión habitual a internet.
- a) Calcula la probabilidad de conectarse habitualmente a internet a través del teléfono móvil.
- b) Si un usuario emplea habitualmente el teléfono móvil para conectarse a internet, halla la probabilidad de que sea propietario de un “Smartphone”.
EJERCICIO PROBABILIDAD 06
En tres máquinas, A, B y C, se fabrican piezas de la misma naturaleza. El porcentaje de piezas que resultan defectuosas en cada máquina es, respectivamente, 1%, 2% y 3%. Se mezclan 300 piezas, 100 de cada máquina, y se elige una pieza al azar, que resulta ser defectuosa. ¿Cuál es la probabilidad de que haya sido fabricada en la máquina A? ver vídeo
EJERCICIO PROBABILIDAD 07
En cierto país donde la enfermedad X es endémica, se sabe que un 12% de la población padece dicha enfermedad. Se dispone de una prueba para detectar la enfermedad, pero no es totalmente fiable, ya que , da positiva en el 90% de los casos de personas realmente enfermas; y da positiva en el 5% de personas sanas. ¿Cuál es la probabilidad de que esté sana una persona a la que la prueba le ha dado positiva? ver vídeo
Ahora vamos a hacer problemas con probabilidad de fórmulas , son más dificiles que los de diagrama de árbol , caaen menos y valen muy poco en los exámenes
EJERCICIO PROBABILIDAD 08
Ver solución
EJERCICIO PROBABILIDAD 09 Ver solución
DISTRIBUCIÓN BINOMIAL
Informate primero si es parte de tu temario , en muchas comunidad autónomas la distribución binomial no entra en la selectividad EBAU , EVAU Yo te recomiendo que aprendas la fórmula y hagas los ejercicios por la fórmula
EJERCICIO DISTRIBUCIÓN BINOMIAL 01
Un jugador marca el 85% de los penaltis que intenta. Si lanza 8 penaltis calcular la probabilidad de
- a) Marque más de 6 penaltis
- b) Marque al menos 6 penaltis
EJERCICIO DISTRIBUCIÓN BINOMIAL 02
La probabilidad de que un tirador acierte en el blanco es de1/4. Si tira 5 veces calcular la probabilidad de
- a) Que acierte como máximo 2 veces
- b) Que acierte alguna vez
EJERCICIO DISTRIBUCIÓN BINOMIAL 03
Un jugador encesta con probabilidad 0.55. Calcula la probabilidad de que al tirar 6 veces enceste:
- a) 4 veces. b) todas las veces c) ninguna vez ver solución
DISTRIBUCIÓN NORMAL
EJERCICIO DISTRIBUCIÓN NORMAL 01
El peso de los recién nacidos sigue una distribución normal de media 3,5 kg y una desviación típica de 0,5 kg. Calcula la probabilidad de que un recién nacido pese : ver solución
- a) Más de 4 Kg
- b) menos de 3,5 Kg
- c) Más de 3 Kg
- d) Menos de 2,5 Kg
EJERCICIO DISTRIBUCIÓN NORMAL 02
La vida útil de un modelo de pila sigue una ley Normal con una media de 100 horas y desviación típica de 10 horas:
a)¿Qué porcentaje de este modelo de pila tendrá una duración inferior a 120 horas?
- b) Halle la probabilidad de que una pila de este modelo elegida al azar, tenga una duración comprendida entre 90 y 110 horas.
EJERCICIO DISTRIBUCIÓN NORMAL 03
El peso de unas manzanas de una huerta sigue una ley Normal con una media de 150 gramos y desviación típica de 20 gramos:
a)¿Qué porcentaje de estas manzanas tendrá un peso inferior a 115 gramos?
- b) Halle la probabilidad de que una manzana de este huerto elegida al azar, tenga un peso comprendido entre 165 y 220 gramos
Intervalos de confianza
Intervalos de confianza ejercicios resueltos 01
El número de viajes mensuales realizados por los usuarios de una autopista sigue una distribución normal de media desconocida y desviación típica de 6 viajes . Tomada una muestra de 576 usuarios , su media mensual ha resultado ser de 12 viajes . Calcula los intervalos de confianza del 95% y 99% para la media de la población. Ver solución
Intervalos de confianza ejercicios resueltos 02
La edad de los alumnos que el año pasado se matricularon en alguno de los cursos de verano de la Universidad de Cantabria sigue una distribución normal con desviación típica de 7 años . Una muestra aleatoria de 150 alumnos ha dado como resultado una edad media de 25,4 años.
- a) Obtener el intervalo de confianza del 94% para la media de edad de todos los matriculados Ver solución
- b) ¿ Cuál es el tamaño mínimo que debe tener la muestra si deseamos que el error cometido al estimar la media con un nivel de confianza del 92% sea de 0,5? Ver solución
Intervalos de confianza ejercicios resueltos 03
El tiempo que los españoles dedican a ver la televisión los domingos es una variable aleatoria que sigue una distribución Normal de media desconocida y desviación típica 75 minutos. Elegida una muestra aleatoria de españoles se ha obtenido, para la media de esa distribución, el intervalo de confianza (188.18, 208.82), con un nivel del 99%.
- a) Calcule la media muestral y el tamaño de la muestra. Ver solución
- b) Calcule el error máximo permitido si se hubiese utilizado una muestra de tamaño 500 y un nivel de confianza del 96%.Ver solución
Intervalos de confianza ejercicios resueltos 04
Se quiere estimar la proporción de hembras entre los peces de una piscifactoría; para ello se ha tomado una muestra aleatoria de 500 peces, y en ella hay 175 hembras.
- a) Calcule un intervalo de confianza para la proporción de hembras en esta población de peces, con un nivel de confianza del 94%.
- b) A la vista del resultado del muestreo se quiere repetir la experiencia para conseguir un intervalo de confianza con el mismo nivel y un error máximo de 0.02,¿cuál es el tamaño mínimo que debe tener la nueva muestra?
Intervalos de confianza ejercicios resueltos 05
De una muestra aleatoria de 120 alumnos presentados a las Pruebas de Acceso, sólo 15 han resultado no aptos.
- a) Calcule un intervalo de confianza, al 99%, para estimar la proporción de alumnos que han resultado aptos en dicha prueba.
- b) Manteniendo la misma confianza, ¿cuál debe ser el tamaño mínimo de la muestra para estimar la proporción de alumnos aptos, cometiendo un error inferior al 5%?
Intervalos de confianza ejercicios resueltos 06
Para una muestra , de tamaño 81 , de alumnas de segundo de bachillerato se obtuvo una estatura media de 167 cm . Por trabajos anteriores se sabe que la desviación típica de la altura de la población de chicas de segundo de bachillerato es de 8 cm. Ver solución
- a) Determinar el intervalo de confianza para la altura media de la población a un nivel de confianza 90%
- b) cuál es el error máximo que se admite para la media poblacional en la estimación realizada?
Contraste de Hipótesis
En la mayoría de comunidades este tema no entra en la selectividad EBAU , EVAU , informaros antes de estudiarlo si en la vuestra entra , ya que es un tema complicado
Contraste de hipótesis ejercicios resueltos 01
Una compañía de zapatillas ha sacado un nuevo modelo. En su publicidad indican que los atletas de medio fondo pueden disminuir su marca en 4 segundos .Se realizan pruebas a 100 atletas y se observa que el tiempo medio de disminución fue de 3,5 segundos. Se sabe que la distribución de ese tiempo es normal con desviación típica de 4 segundos . Con un nivel de confianza del 95% ¿ podríamos aceptar que la hipótesis de la compañía es cierta ?
Contraste de hipótesis ejercicios resueltos 02
Una compañía de zapatillas ha sacado un nuevo modelo. En su publicidad indican que los atletas de medio fondo pueden disminuir su marca en 4 segundos .Se realizan pruebas a 100 atletas y se observa que el tiempo medio de disminución fue de 3,5 segundos. Se sabe que la distribución de ese tiempo es normal con desviación típica de 4 segundos . Con un nivel de confianza del 95% ¿ podríamos aceptar que la hipótesis de la compañía es cierta ?
