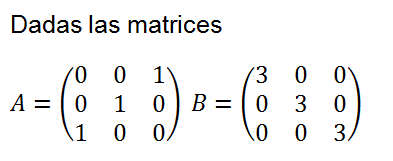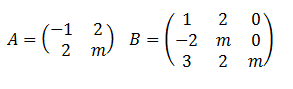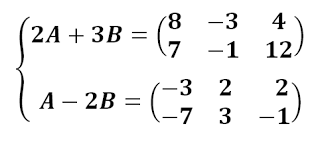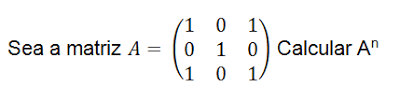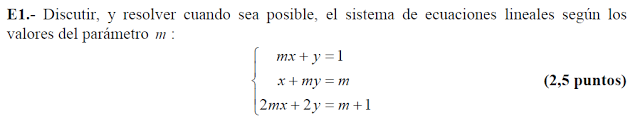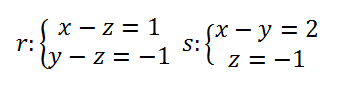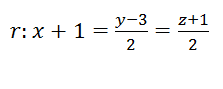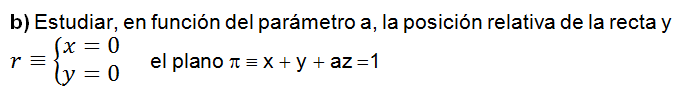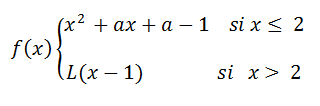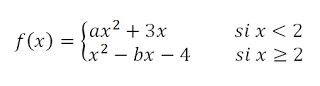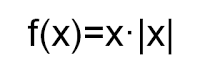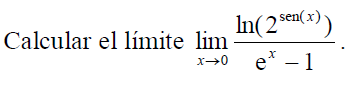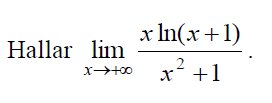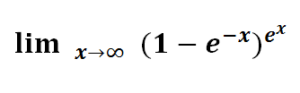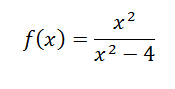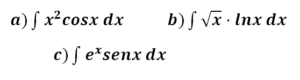Ejercicios y problemas resueltos de exámenes , pdf , matemáticas 2º bachillerato ,
para preparar el examen final de MATEMÁTICAS de segundo de bachillerato , y
también la selectividad . Si ves que flojeas en algún tema estudiarlo en el curso
para aprobar MATEMATICAS de 2º de bachillerato .
TEMA MATRICES Y DETERMINANTES
01
02 EBAU EVAU
Ver parte 1 ver parte 2 ver parte 3
03 EBAU EVAU
a) Encuentra el valor , o los valores, de m para los que las matrices A y B tienen el mismo rango
b)Determinar , si existen , los valores de m para los que A y B tienen el mismo determinante
T
TEMA SISTEMAS DE ECUACIONES
Los sistemas de ecuaciones son un CLASICO DE EXAMEN , casi siempre caen , sobre todo los 3×3 , en este repaso os he dejado tres ejercicios de 3×3 y luego con otras dimensiones que también pueden caer .
Ejercicio 01 sistemas de ecuaciones con parámetros
Discutir y resolver el sistema siempre que sea posible
Ejercicio 02 sistemas de ecuaciones con parámetros EVAU EBAU
Ejercicio 03 sistemas de ecuaciones con parámetros EBAU EVAU
Ejercicio 04 sistemas de ecuaciones con parámetros EBAU EVAU SISTEMA3X2
Ejercicio 05 sistemas de ecuaciones con parámetros EBAU EVAU SISTEMA2X2
https://www.youtube.com/c/profesor10experimentos
TEMA GEOMETRÍA
MUY IMPORTANTE repasar todas las fórmulas de distancias, ángulos y los rangos para las posiciones relativas , SIEMPRE cae alguna pregunta que solo hay que aplicar la fórmula , deben ser puntos fijos . También repasar los ejercicios clásicos , perpendicular común y los simétricos .
Ejercicio de geometría 01
Calcular un vector unitario y ortogonal a v=(1,2,0,) y w=(-1,0,1)
Ejercicio de geometría 02
Estudiar la posición relativa entre las rectas
Ejercicio de geometría 03 EBAU EVAU
Dadas las rectas
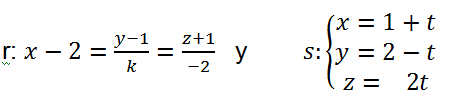
Hallar k para que las rectas sean coplanarias ver parte 1 ver parte 2
Ejercicio de geometría 04 EBAU EVAU
Calcular la distancia del punto P(1,0,-2) al plano π:-2x+3y+2z-1=0
Ejercicio de geometría 05 EBAU EVAU
ver solución
Ejercicio de geometría 06 EBAU EVAU
Calcular la recta que corta perpendicularmente al eje OZ y que pasa por el punto P = (1, 2,3) ver solución
Ejercicio de geometría 07 EBAU EVAU
Ejercicio de geometría 08EBAU EVAU
Determínese el punto simétrico de P(1,1,1) respecto al plano π: x-y+z=5
Ahora vamos a hacer un par de ejercicios de lo más complicado de este tema , los ejercicios de punto genérico
Ejercicio de geometría 09 EBAU EVAU
Sean el plano π:x+y+z=0 la recta r: x=y=z y el punto A(3,2,1) , hallar el punto de r que equidista de A y π
FUNCIONES
Para estos temas es muy importante , que sepas derivar perfectamente , y también que sepas calcular perfectamente los dominios de las funcionesOJO con los dominios
Funciones ejercicios 01
Funciones ejercicios 02
Probar que las gráficas f(x)=ex y g(x)=1/x se cortan en algún punto x>0
Funciones ejercicios 03
Funciones ejercicios 04
Funciones ejercicios 05
Funciones ejercicios 06
Calcular a , b , c para que la función f(x) cumpla las hipótesis del teorema de Rolle en el intervalo [0,4] ¿ en qué punto cumple la tesis ?
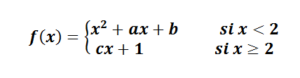
https://www.youtube.com/c/profesor10experimentos
Funciones ejercicios 07
Resuelve los límites
 ver solución
ver solución
Funciones ejercicios 08
ver solución
Optinización de funciones , probablemente una de las partes más complicadas de la asignatura , os dejo un par de ejercicios clásicos , pero recordar que en siguiente enlace teneis unos cuantos ejercicios más . darle caña que son ejercicios clásicos Aqui tienes el enlace al curso para ser una máquina de optimización de funciones
Funciones ejercicios 09
Una caja con tapa y base cuadrada debe tener un volumen de 160 cm3. El precio del material utilizado para la base es de 3 euros por centímetro cuadrado, y el utilizado para las caras laterales y la tapa es de 2 euros por centímetro cuadrado. Calcula las dimensiones de la caja para que resulte lo más económica posible.
Funciones ejercicios 10
1 http://youtu.be/pPHA_xSlryM
Funciones ejercicios 11
Se desea construir un depósito con forma de prisma rectangular de base cuadrada y con una capacidad de 360 m3. Los costes por m2 son los siguientes: 40 € para el fondo, 30 € para las paredes laterales y 60 € para el techo del depósito. Calcula las dimensiones del depósito para que su coste sea el menor posible.
Funciones ejercicios 12
Calcula las dimensiones de un rectángulo inscrito en un semicírculo de 10 cm de radio , para que su área sea máxima
Ahora vamos a hacer un expecial de representación gráfica de funciones,en selectividad EBAU EVAU , no suelen pedir todos los apartados , pero yo prefiero calularlos todos para que repaseis ( en el examen hacer solo lo que os piden , como mucho a mayores calcular los puntos de corte) , recordar que para dibujar una función yo me fijo expecialmente en el DOMINIO , ASÍNTOTAS, EXTREMOS RELATIVOS Y PUNTOS DE COTRTE CON LOS EJES
Por si lo necesitas te dejo el enlace al curso para ser una máquina de representación gráfica de funciones
Funciones ejercicios 13
Funciones ejercicios 14
Representa gráficamente f(x)=(x+2)·e-x
Ver dominio , simetría y puntos de corte
Ver curvatura y Puntos de Inflexión
Funciones ejercicios 15
Representar la siguiente función
f(x)=lnx/x
Ver monotonía y extremos relativos
Ver curvatura y puntos de inflexión
https://www.youtube.com/c/profesor10experimentos
INTEGRALES
Sin lugar a dudas lo más complicado del temario , acordaros que las integrales inmediatas seguramente sean las más dificiles , llevar bien los métodos de integración , por partes , racionales y cambio de variable , las áreas y el cálculo de primitivas que suelen ser ejercicios un poco más fáciles . Aqui te dejo el enlace al curso para ser unas máquinas de las integrales por si lo necesitas
Ejercico de Integrales 01
Resuelve estas 10 integrales , si consigues hacer bien 8 o más dimelo en los comentarios y e doy el título de máquina de integrales inmediatas

Ejercico de Integrales 02
Ejercico de Integrales 03
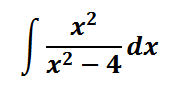
Ejercico de Integrales 04
Calcular el área de la región limitada por f(x) = x2 -1, el eje OX y las rectas x=0 y x=2
Ejercico de Integrales 05
Calcular el área delimitada por la parábola de ecuación y=2x2 la recta y=2x+4
Ejercico de Integrales 06
Calcular el área de la región delimitada por la gráfica de la función f(x)=lnx , el eje OX y la recta x=3 ver solución
Ejercico de Integrales 07
Consideremos la función f(x)=x3+mx2+1 con m≥0 . Calcular el valor de m para que el área del recinto limitado por la gráfica de la función f(x) , el eje OX y las rectas x=0 y x=2 sea 10 ver solución
Ejercico de Integrales 08
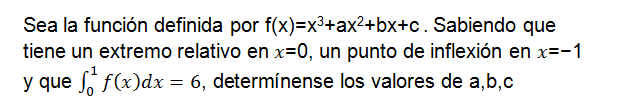
Ejercico de Integrales 09
PROBABILIDAD
EJERCICIO PROBABILIDAD 01
En una bolsa hay cuatro bolas rojas y una verde. Se extraen de forma consecutiva y sin reemplazamiento dos bolas. Calcúlese la probabilidad de que:
- a) Las dos bolas sean del mismo color.
- b) La primera bola haya sido verde si la segunda bola extraída es roja.
EJERCICIO PROBABILIDAD 02
Un moderno edificio tiene dos ascensores para uso de los vecinos. El primero de los ascensores es usado el 45% de las ocasiones, mientras que el segundo es usado el resto de las ocasiones. El uso continuado de los ascensores provoca un 5% de fallos en el primero de los ascensores y un 8% en el segundo. Un día suena la alarma de uno de los ascensores porque ha fallado. Calcula la probabilidad de que haya sido el primero de los ascensores.
EJERCICIO PROBABILIDAD 03
La lista electoral de un determinado partido político está formada por un número igual de hombres y mujeres. Un análisis sociológico de dichas listas revela que el 60% de los hombres tienen 40 o más años de edad, mientras que el 30% de las mujeres tienen menos de 40 años. Se elige al azar una persona que forma parte de las listas electorales.
- a) Calcula la probabilidad de que tenga menos de 40 años.
- b) Sabiendo que tiene 40 o más años de edad, calcula la probabilidad de que sea mujer.
EJERCICIO PROBABILIDAD 05
Según el informe anual La Sociedad de la Información 2012, el 63% de los usuarios de móvil en España tiene un “Smartphone”. Entre los propietarios de este tipo de teléfono, el 77% lo emplea para su conexión habitual a internet. Sin embargo, entre los propietarios de otros tipos de teléfono móvil sólo el 8 % lo emplea para la conexión habitual a internet.
- a) Calcula la probabilidad de conectarse habitualmente a internet a través del teléfono móvil.
- b) Si un usuario emplea habitualmente el teléfono móvil para conectarse a internet, halla la probabilidad de que sea propietario de un “Smartphone”.
DISTRIBUCIÓN NORMAL
EJERCICIO DISTRIBUCIÓN NORMAL 01
El peso de los recién nacidos sigue una distribución normal de media 3,5 kg y una desviación típica de 0,5 kg. Calcula la probabilidad de que un recién nacido pese : ver solución
- a) Más de 4 Kg
- b) menos de 3,5 Kg
- c) Más de 3 Kg
- d) Menos de 2,5 Kg
EJERCICIO DISTRIBUCIÓN NORMAL 02
La vida útil de un modelo de pila sigue una ley Normal con una media de 100 horas y desviación típica de 10 horas:
a)¿Qué porcentaje de este modelo de pila tendrá una duración inferior a 120 horas?
- b) Halle la probabilidad de que una pila de este modelo elegida al azar, tenga una duración comprendida entre 90 y 110 horas.
EJERCICIO DISTRIBUCIÓN NORMAL 03
El peso de unas manzanas de una huerta sigue una ley Normal con una media de 150 gramos y desviación típica de 20 gramos:
a)¿Qué porcentaje de estas manzanas tendrá un peso inferior a 115 gramos?
- b) Halle la probabilidad de que una manzana de este huerto elegida al azar, tenga un peso comprendido entre 165 y 220 gramos
DISTRIBUCIÓN BINOMIAL
Informate primero si es parte de tu temario , en muchas comunidad autónomas la distribución binomial no entra en la selectividad EBAU , EVAU Yo te recomiendo que aprendas la fórmula y hagas los ejercicios por la fórmula
EJERCICIO DISTRIBUCIÓN BINOMIAL 01
Un jugador marca el 85% de los penaltis que intenta. Si lanza 8 penaltis calcular la probabilidad de
- a) Marque más de 6 penaltis
- b) Marque al menos 6 penaltis
EJERCICIO DISTRIBUCIÓN BINOMIAL 02
La probabilidad de que un tirador acierte en el blanco es de1/4. Si tira 5 veces calcular la probabilidad de
- a) Que acierte como máximo 2 veces
- b) Que acierte alguna vez
Para seguir al profesor10demates , recibir todas las novedades y consultarle dudas podéis SUSCRIBIROS y retwiterame en las siguientes redes sociales: