Simétrico de un punto P respecto a una recta r . Geometría en el espacio Fórmulas ejercicios resueltos , , 2 bachillerato , pruebas de acceso , selectividad
Simétrico de un punto P respecto a una recta r
Calculamos el plano π que pasa por el punto P y es perpendicular a la recta r
Calculamos el punto I . Intersección del plano π con la recta r ( el punto I es la proyección del punto P sobre la recta r)
Ejercicio resuelto
Si los videos te han servido , dale al 🔥 LIKE y SUSCRíBETE y activa la campanilla 🔔, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
CURSOS
Matemáticas 2º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias aplicadas a las ciencias sociales

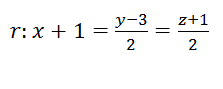
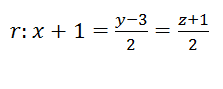







3 comentarios
que decirte….eres un mago….
ya sabes lo que decía Einstein….
no entiendes una cosa hasta que no eres capaz de explicársela a tu abuela… Mi abuela sabría Geometría Espacial contigo
haces fácil lo difícil
eres muy bueno
Enhorabuena
(y se bien de qué hablo)
Jajajajaaja , muchísimas gracias
Gracias, y enhorabuena por los resultados de los vídeos. Me estás ayudando con mates para exámenes de acceso a la academia básica militar. Y espero que tus temas de física sean también tan buenos como los de mates.
Por otra parte. Cómo crítica constructiva, ha pensado en hacer vídeos en pizarras de rotulación?? Creo que aún sería más visual, más cognitivos….Creo que veríamos las cosas más fácilmente aún…
Gracias x todo.