Diagonalización de matrices ejercicios y problemas resueltos paso a paso de diagonalizar matrices , valores y vectores propios , autovalores y autovectores, polinomio característico , diagonalización de endomorfismos , matriz de paso y matriz semejantes
lista de reproducción de diagonalización
Antes de empezar con el tema de diagonalización de matrices es muy importante que dominéis ciertos temas como :
rangos por matrices , determinantes, ecuaciones de 2 grado y Ruffini y sobre todo , resolución de sistemas compatibles indeterminados por Gauss , os dejo los enlaces para que lo trabajéis, DIAGONALIZACIÓN conocimientos previos
Diagonalización de matrices en R
Pasos a seguir
1 Calculamos el polinomio característico de A
2 Calculamos los valores propios o autovalores, con su multiplicidad algebraica (Si todos son reales la matriz puede ser diagonalizable)
3 Calculamos los vectores propios o autovectores , de los subespacios propios con su multiplicidad geométrica
4 Si la multiplicidad algebraica de los valores propios o autovalores es igual a la multiplicidad geométrica la matriz A es diagonalizable
5 Si la matriz A es diagonalizable calculamos las matrices D y P.Siendo D la matriz diagonal semejante a A y P la matriz de paso
Propiedad
Si la multiplicidad algebraica de un autovalor es uno ; la multiplicidad geométrica también será uno
Ejemplo 1
Determinar si la matriz A es diagonalizable y en caso afirmativo determinar la matriz D y P
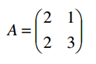
Ejemplo 2
Determinar si la matriz es diagonalizable y en caso afirmativo determinar la matriz D y P
OTROS TEMAS QUE TE PUEDEN INTERESAR


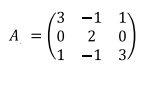







24 comentarios
Hola Sergio. no consigo ver todos los videos. solo el primero de cada ejercicio.
mir en esta enlace https://www.youtube.com/playlist?list=PLunRFUHsCA1ypG4CT7stnRNS1qWQll5ep
Gracias Sergio, con el portatil pude verlo… fue tema de la tablet.
Eres un crak… muy bien explicado.
Gracias Olga ,
Cambiaré los enlaces para que todo el mundo pueda verlos
saludos
Genial, muchas gracias por tu trabajo. Gracias a tus vídeos creo que voy a poder aprobar álgebra por fin! El libro que nos han mandado estudiar como texto base de la asignatura en la UNED es un horror, pero afortunadamente descubrí tu blog, y ha sido un verdadero salvavidas.
Siempre doy a Me gusta y estoy suscrita a tu canal. Verdaderamente eres un profesor 10!
Hola Sergio, primeramente de todo gracias por hacer del algebra una asignatura tan facil tus videos son super aclaratorios! Bien estoy estudiando para la convocatoria que tengo este 1 de septiembre y me topado con un ejercicio al cual no se como cogerle mano, te lo explico: Me piden que estudie si una matriz es diagonalizable en funcion de la letra a, la matriz es la siguiente,
0 -a a
A= 0 -1 1
0 -a a
¿Como podría hacerlo?
Saludos y muchas gracias por tu tiempo!
lo siento Fernando , pero ando muy liado y no voy a poder ayudarte ,
el ejercicio es muy complicado para poder resolverlo aquí
tengo un ejerciio de diagonalización con parámetros resuelto en esta entrada
buscalo y si no lo ves me lo dices
https://www.youtube.com/playlist?list=PLunRFUHsCA1xq3fV5_DaG-ILtm9MeIgWo
¡Sergio tienes mi gratitud eterna, he logrado entender el algebra y al final he aprobado el examen, tu si que eres un profesor10!
Enhorabuena
Tenemos que estudiar este tema por nosotrxs mismxs en la universidad y me lo has aclarado 100%. Es más, me has resuelto alguna duda que tenía con la resolución de los vectores propios. Enhorabuena 😉
hola Sergio! antes de todo te doy las gracias por los videos. han sido de gran ayuda para que muchos aproeben sus asignaturas.
y ahora quiero pedirte que grabaras unos videos de ortogonalidad y formas bilineales y cuadraticas de la asignatura de álgebra de la UNED si es posible. sere muy agradecido.
muchas gracias,
un saludo
Hola Sergio, por casualidad no tendrías algún vídeo sobre la diagonalización de matrices 4×4, gracias,
Lo siento No
Lo siento No
Te sugiero simplificarla por adjuntos y transformarla en un determinante de 3×3, Sergio tiene videos donde lo explica muy bien
Muchísimas gracias por tus vídeos Sergio, son de gran ayuda.
Sergio, por casualidad no tendras videos o apuntes de conicas y cuadricas, no? Es q tengo que explicar yo el temario delante de mis compañeros y ne prifesor y no se como
lo siento no tengo
Hola sergio
hola Sergio !!!!!!!!!!!!!!!!!!! eres un crack muchas gracias por los enlaces, estas consiguiendo que disfrute muchísimo con álgebra y calculo, no hay suficientes "me gustas" para agradecértelo, un saludo!!!!!!!!!!!!!!!!!!!
podrias subir mas ejercicios y complicar mas la cosa?
no voy a volver a pisar una clase de algebra de lo que queda del curso. QUE CRACK ERES SERGIO.
Hola Sergio, Podrías ampliar el temario de álgebra?? Muchas gracias!!! Eres un crack!!!
Hola Sergio, tienes algún video del proceso de Diagonalización de matrices 4×4 u otro ejemplo del 3×3 (que no tenga 2 ceros en una misma fila). No me quedó muy claro cuando tomaste ese atajo. Muchas gracias