Inferencia estadística 1 , 2 bachillerato y universidad .
Intervalo de confianza para la media poblacional
![]()
Siendo
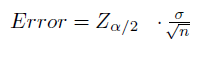
Tamaño de la muestra :
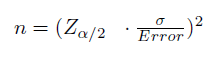
Zα/2 un parámetro que se calcula con el nivel de confianza ( es muy importante aprenderlo a calcular bien , en los siguientes videos veremos como se calcula )
Ejercicioparte 1parte 2parte 3
Calcular Zα/2 en los siguientes apartados
a) Con un nivel de confianza del 95%
b) Con un nivel de confianza del 99% y del 90%
c) con un nivel de significación del 2% y 7%
d) Con α=0,03
Intervalo de confianza para la media ejercicios resueltos
Ejercicio 01 Selectividad matemáticas aplicadas a las ciencias sociales
El número de viajes mensuales realizados por los usuarios de una autopista sigue una distribución normal de media desconocida y desviación típica de 6 viajes . Tomada una muestra de 576 usuarios , su media mensual ha resultado ser de 12 viajes . Calcula los intervalos de confianza del 95% y 99% para la media de la población. Ver solución
Intervalos de confianza Ejercicio resuelto Examen PAU 2025
El número de días de permanencia de los enfermos en un hospital sigue una ley Normal de media desconocida y desviación típica 3 días.
i) (25 puntos) Determine un intervalo de confianza para estimar la media poblacional, a un nivel de confianza del 97%, con una muestra aleatoria de 100 enfermos cuya media es 8.1 días.
ii) (25 puntos) ¿Qué tamaño mínimo debe tener una muestra aleatoria para poder estimar la media poblacional con un error inferior a 1 día y un nivel de confianza del 92%?
Ejercicio 02 Selectividad matemáticas aplicadas a las ciencias sociales
Para una muestra , de tamaño 81 , de alumnas de segundo de bachillerato se obtuvo una estatura media de 167 cm . Por trabajos anteriores se sabe que la desviación típica de la altura de la población de chicas de segundo de bachillerato es de 8 cm. Ver solución
a) Determinar el intervalo de confianza para la altura media de la población a un nivel de confianza 90%
b) cuál es el error máximo que se admite para la media poblacional en la estimación realizada?
03 Selectividad matemáticas aplicadas a las ciencias sociales
La edad de los alumnos que el año pasado se matricularon en alguno de los cursos de verano de la Universidad de Cantabria sigue una distribución normal con desviación típica de 7 años . Una muestra aleatoria de 150 alumnos ha dado como resultado una edad media de 25,4 años.
a) Obtener el intervalo de confianza del 94% para la media de edad de todos los matriculados Ver solución
b) ¿ Cuál es el tamaño mínimo que debe tener la muestra si deseamos que el error cometido al estimar la media con un nivel de confianza del 92% sea de 0,5? Ver solución
04 Ejercicio clásico de examen
En verano, en Madrid, se instalan puestos callejeros de venta de melones y sandías. Se sabe que el peso de las sandías puede aproximarse por una variable con distribución normal de media µ y desviación típica σ = 450g. a) Si se toma una muestra de 25 sandías y se obtiene una media muestral de 2,7 Kg , calcule un intervalo de confianza al 95 % para la media poblacional. b) Si el peso medio de las sandías es µ = 3000g, calcule la probabilidad de que una muestra de cuatro sandías cogidas al azar pese en media entre 3000g y 3450g. ver solución
Si los videos te han servido , dale al LIKE y SUSCRIBETE 🚂 http://goo.gl/CMFnu0 y activa la campanilla🔥, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
Más ejercicios de Intervalos de confianza resueltos de exámenes
Ejercicio 05
La duración en horas de un determinado tipo de bombillas se puede aproximar por una distribución normal de media µ y desviación típica igual a 1940 h. Se toma una muestra aleatoria simple.
a) Qué tamaño muestral se necesitará como mínimo para que, con nivel de confianza del 95 %, el valor absoluto de la diferencia entre µ y la duración media observada de esas bombillas sea inferior a 100 h? solución
b) Si el tamaño de la muestra es 225 y la duración media observada X es de 12415 h, obténgase un intervalo de confianza al 90% para µ ver solución
Ejercicio 06
El número de megabytes (Mb) descargados mensualmente por el grupo de clientes de una compañía de telefonía móvil con la tarifa AA se puede aproximar por una distribución normal con media 3,5Mb y una desviación típica igual a 1,4Mb. Se toma una muestra aleatoria de tamaño 24.
a)Cuál es la probabilidad de que la media muestral sea inferior de 3,37Mb?.solución
b) Supóngase ahora que la media poblacional es desconocida y que la media muestral toma el valor de 3,42 Mb. Obténgase un intervalo de confianza al 95% para la media de la población. Ver solución
Ejercicio 07
El tiempo que los españoles dedican a ver la televisión los domingos es una variable aleatoria que sigue una distribución Normal de media desconocida y desviación típica 75 minutos. Elegida una muestra aleatoria de españoles se ha obtenido, para la media de esa distribución, el intervalo de confianza (188.18, 208.82), con un nivel del 99%.
- a) Calcule la media muestral y el tamaño de la muestra. Ver solución
- b) Calcule el error máximo permitido si se hubiese utilizado una muestra de tamaño 500 y un nivel de confianza del 96%.Ver solución
Ejercicio 08
Una fábrica produce cables de acero, cuya resiliencia sigue una distribución normal de media desconocida y desviación típica σ=10 KJ/m3. Se tomó una muestra de 100 piezas y mediante un estudio estadístico se obtuvo un intervalo de confianza (898,04, 901,96) para la resiliencia media de los cables de acero producidos en la fábrica.
- a) Calcula el valor de la resiliencia media de las 100 piezas de la muestra. Ver solución
- b) Calcula el nivel de confianza con el que se ha obtenido dicho intervalo.
Ejercicio 09
El tiempo de reacción ante un obstáculo imprevisto de los conductores de automóviles de un país, en milisegundos (ms), se puede aproximar por una variable aleatoria con distribución normal de media μ desconocida y desviación típica σ = 250 ms.
a) Se toma una muestra aleatoria simple y se obtiene un intervalo de confianza (701; 799), expresado en ms, para μ con un nivel del 95 %. Calcúlese la media muestral y el tamaño de la muestra elegida.
b) Se toma una muestra aleatoria simple de tamaño 25. Calcúlese el error máximo cometido en la estimación de μ mediante la media muestral con un nivel de confianza del 80 %. Ver parte a ver parte b
enlaces a nuestros CURSOS gratis que te pueden interesar
Matemáticas 2º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias aplicadas a las ciencias sociales
UNIVERDIDAD Matemáticas Física Química y Estadística









8 comentarios
Sergio…
¡No nos dejes así! Vamos, un pequeño esfuerzo, que la matanza llegará pronto, jajajaja…
En serio, si pudieras seguir un poco más, nos ahorraremos bastante en velas, seguro.
Gracias por todo.
Ando muy liado , si tengo tiempo intentaré seguir desarrollando temas
Supongo, Sergio, que como el zapato de un romano, seguro.
De todas formas te prometemos millones de "me gusta". El manual oficial es infumable, de verdad.
Insisto (y creo que hablo por todos) en el agradecimiento. Si no fuera por tus videos se haría verdad la frase de Dante.
¿El de la UNED? iNFUMABLE es poco. Gracias de Nuevo, Sergo.
Hola,
Gracias por este fantástico blog.
¿El tema 6 que publicas aquí es el tema 7 del temario oficial (estadistica empresarial Grado ADE Uned)? Lo digo por la coincidencia del nombre con el tema 7.
En cuanto a los últimos temas, que como comentaste no tendrás tiempo, ¿Podrías recomendar algún consejo o video por la red?
Muchisimas gracias.
Eres grande
Muchisimas Sergio. Cóbranos lo que sea, pero no nos dejes. Eres el mejor.
que crack. Gracias por todo picha !!