Tipificación N(μ,σ)
Distribución normal ejercicios resueltos
Vamos a realizar 3 ejercicios que son clásicos de examen y aprovecharemos para trabajar ciertos conceptos trucos y claves y así dominaremos el tema ver vídeo
Ejercicio resuelto clásico de examen de Distribución Normal 01
La temperatura del cuerpo humano sigue una distribución normal de media 37ºC y desviación típica 0,5ºC.
a) Calcular la probabilidad de que la temperatura de una persona sea menor que 36,5ºC
b) Calcular la probabilidad de que la temperatura de una persona sea mayor que 36ºC
c) Calcular la probabilidad de que la temperatura de una persona esté comprendida entre 36ºC y 38ºC
Ejercicio resuelto clásico de examen de Distribución Normal 02
Las notas de Matemáticas II de 500 alumnos presentados al examen de EBAU tienen una distribución normal con media 6,5 y varianza 4.
a) Calcule la probabilidad de que un alumno haya obtenido más de 8 puntos.
b) ¿Cuántos alumnos obtuvieron notas menores de 4 puntos?
Ejercicio resuelto clásico de examen de Distribución Normal 03
En un instituto la altura media es de 1,78 m con una desviavión típica de 20 cm . Si elegimos un alumno al azar calcula la probabilidad de :
a) Mida más de 1,85 m
b) Mida menos de 1,7 m
c) Mida entre 1,75 m y 1,9 m
Ejercicios clásicos de examen nivel full
En los últimos años este tipo de ejercicios se han convertido en súper clásicos de examen , así que vamos a meterle caña , ya sabes si en clase pronto tenéis examen compártelo en los grupos de clases VAMOS A POR NOTAZA !!!
Ejercicio clásico de examen Full
El tiempo empleado, en minutos, para obtener la respuesta de un test para detectar cierta enfermedad sigue una distribución normal de media 20 y de desviación típica 4.
a) ¿En qué porcentaje de test se obtiene el resultado entre 16 y 26 minutos?
b) ¿Cuántos minutos son necesarios para garantizar que se ha obtenido la respuesta del 96.41% de los test?
c) ¿Cuántos minutos son necesarios para garantizar que se ha obtenido la respuesta del 37,45% de los test?
Ejercicio clásico de examen calcular nota de corte
Las notas que se han obtenido por 1000 opositores han seguido una distribución normal de media 4,05 y desviación típica 2,5. a) ¿Cuántos opositores han superado el 5?
b) Si tenemos que adjudicar 330 plazas, calcula razonadamente la nota de corte.
Ejercicio clásico de examen como calcular la media de una distribución normal
La velocidad de los vehículos en una autopista con límite de velocidad de 120 km/h sigue una distribución normal de media µ km/h y desviación típica s =10 km/h. Se sabe que el 69,15% de los vehículos no sobrepasan la velocidad de 130 km/h
a) Calcule la media de esta distribución.
b)¿Cuál es el porcentaje de vehículos que no sobrepasan la velocidad máxima permitida?
c) La DGT establece una multa de 100 euros a los vehículos que viajan entre 120 y 150 km/h ¿Cuál es la probabilidad de ser sancionado con dicha multa?
Ejercicio clásico de examen como calcular la desviación típica de una distribución normal
Una empresa ha llevado a cabo un proceso de selección de personal. Las puntuaciones obtenidas por los aspirantes en el proceso de selección siguen una distribución normal, X, de media 5.6 y desviación típica σ. Sabiendo que la probabilidad de obtener una puntuación X ≤ 8.2 es 0.67, calcule σ.
normal de media 20 y desviación típica 2,5. Calcula la probabilidad de que en
una semana se presten entre 15 y 25 libros.
Problema
4 Prueba de acceso mayores de 25 años universidad CAD Matemáticas aplicadas a las ciencias sociales
5 Prueba de acceso mayores de 25 años universidad CAD Matemáticas aplicadas a las ciencias sociales
7 Selectividad ( PAU ) Castilla y León Matemáticas ciencias sociales Septiembre 2010 General
8 Selectividad ( PAU ) Castilla y León Matemáticas ciencias sociales Septiembre 2013

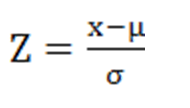
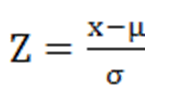
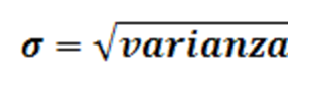







Un comentario
Muchisimas gracias, por el esfuerzo de explicar todo tan bien y con tan buen humor. Para mi hasta que hice tu curso la distribución normal y binomial me daba pavor y ahora creo que puedo con ella.
Muchas gracias y sigue así.