ejercicios y problemas resueltos con solución en vídeo de derivación de funciones de varias variables
¡¡ MUY IMPORTANTE ¡¡ Ver explicación
Antes de empezar con las derivadas de funciones de varias variables tenemos que dominar las derivadas de una variable , sino es vuestro caso ir al siguiente enlace DERIVADAS
Ejercicio 1 Calcular las derivadas parciales de :
a) f(x,y)=x2+y2-6x+3y
b) f(x,y)=3×2+4y2-7x+8y
Ejercicio 2 Calcular las derivadas parciales de :
a) f(x,y)=x2+2y+3xy2
b) f(x,y)=2×2-4x2y+5y
Ejercicio 3 Calcular las derivadas parciales de :
a) f(x,y)=4×2+3xy2-6x2y
b) f(x,y)=3×2-6x2y3+3xy
Ejercicio 4 Calcular las derivadas parciales de :
f(x,y,z)=x2-4xy+z2-3xz
Ejercicio 5 Calcular las derivadas parciales de :
a) f(x,y,z)=x3-2xz-3yz2+4xyz
Ejercicio 6 Calcular las derivadas parciales de :
a)f(x,y,z)=x2y-6xz+2xy2z
Ejercicio 7 Calcular las derivadas parciales de :
a) f(x,y,z)=x3+y2+6z-3xy2+x2y2z2
Ejercicio 8 Calcular las derivadas parciales de :
Ejercicio 9 Calcular las derivadas parciales de :
Ejercicio 10 Calcular las derivadas parciales de :
Ejercicio 11 Calcular las derivadas parciales en el punto P(0,1) de :
f(x,y)= x3-3x2y+2xy2

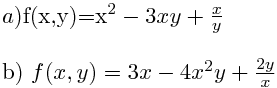
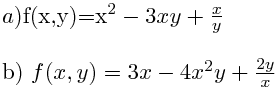
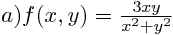
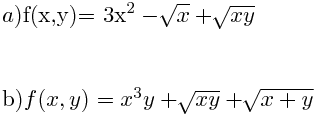







6 comentarios
Sergio, los enlaces del 9 y el 10 los tienes cambiados. Gracias por tu blog
gracias luego cambio los enlaces
Muchas gracias por tus clases, son geniales… a sí apruebo a la primera 🙂
Es una excelente explicación, podrías hacer algún ejemplo utilizando e (exponencial) elevado a `y` o `x`
seria posible que realizaras un tutorial y explicacion acerca de optimizacion y bosquejo de curva es q me urge para la finalizacion de mi semetre!!!! te lo agradeceria
gracias, por esta pagina voy a pasar mi extraordinario de calculo vectorial