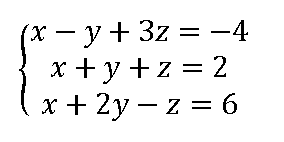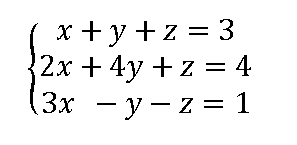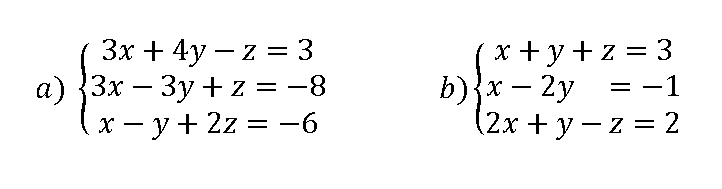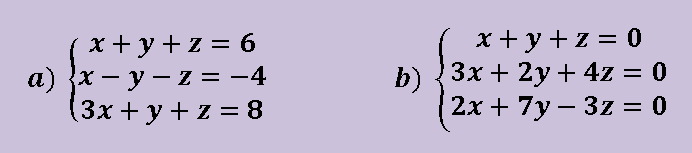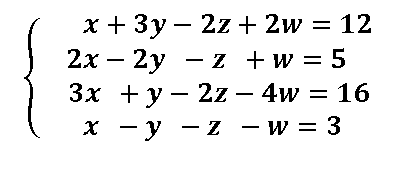Ejercicios Resueltos paso a paso , Método de Gauss sistemas de ecuaciones lineales 3×3 , 4×4 explicación de ejemplos desde cero . Aprenderemos a clasificar y a resolver Sistemas Compatibles Determinados SCD , Sistemas Compatibles Indeterminados SCI y Sistemas Incompatibles SI
Método de Gauss Sistemas de ecuaciones
Para resolver sistemas de ecuaciones por el método de Gauss , seguiremos los siguientes pasos
Paso 1 (lo veremos explicado detalladamente en los vídeos), obtenemos un sistema equivalente escalonado reducido
Paso 2 (lo veremos explicado detalladamente en los vídeos)
Una vez obtenido el sistema escalonado iremos de abajo a arriba obteniendo las soluciones
Método de Gauss sistemas de ecuaciones 3×3
Ejercicio resuelto 01 Resuelve el siguiente sistema de ecuaciones
Ejercicio resuelto 02 ver solución
Resuelve los siguientes sistemas de ecuaciones
Ahora te toca practicar , resuelve los siguientes sistemas y abre el vídeo para corregirlos , muy importante aprende de los errores y si los haces bien ponte un MB 😉
Ejercicio resuelto 03
Resuelve los siguientes sistemas de ecuaciones
Apartado a) parte 1 parte 2 Apartado b) parte 1 parte 2
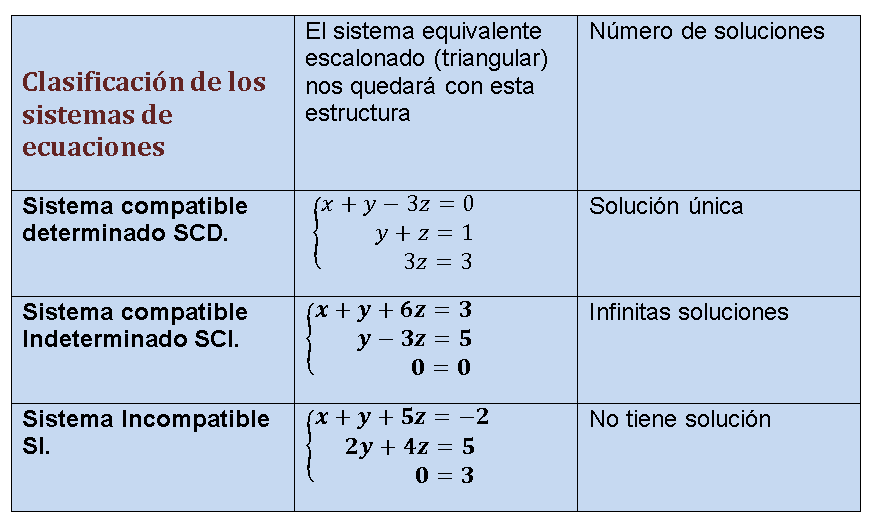
Clasificación de los sistemas de ecuaciones
La clasificación de sistemas de ecuaciones y su resolución va a ser muy importante a partir de ahora en nuestra “vida matemática” Así que vamos a meterle caña para transformarnos en máquinas .Siempre vamos a tener que clasificar el sistema y luego resolverlo.
IMPORTANTE VER EXPLICACIÒN
Clasificación de los sistemas de ecuaciones Dependiendo del número de soluciones
Sistemas compatibles determinados SCD.
Tienen una única solución.
El sistema equivalente escalonado (triangular) nos quedará con esta estructura
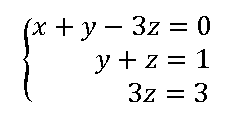
Sistemas compatibles Indeterminados SCI.
Tienen infinitas soluciones
El sistema equivalente escalonado (triangular) nos quedará con esta estructura
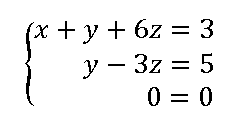
Sistemas Incompatibles SI.
No tienen solución
El sistema equivalente escalonado (triangular) nos quedará con esta estructura
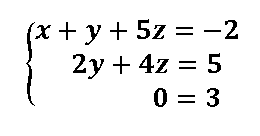
También podemos clasificar los sistemas en :
a) Homogéneos . Son sistemas de ecuaciones lineales donde TODOS sus términos independientes son 0
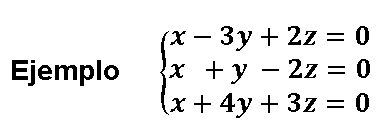
Los sistemas Homogéneos, tienen dos propiedades muy interesantes
1) El sistema siempre es Compatible (Determinado o Indeterminado)
2) Si el sistema es compatible determinado, tiene la solución trivial, que es aquella en las que todas sus soluciones son cero : x=0 , y=0 , z=0
b) Heterogéneos Cuando No son homogéneos
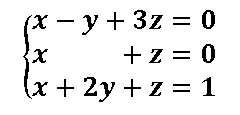
Ejercicios resueltos Sitemas Compatibles Indeterminados
Clasifica y resuelve los siguientres sistemas de ecuaciones por el método de Gauss
Ver solución apartado a ver solución apartado b
Ejercicios resueltos Sitemas Incompatibles
Clasifica y resuelve los siguientres sistemas de ecuaciones por el método de Gauss ver solución
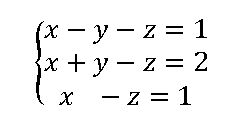
Ejercicios para practicar Ahora te toca a ti 😉 clasifica y resuelve los siguientes sistemas y comprueba la solución con los vídeos
Apartado a parte 1 parte 2 Apartado b parte 1 parte 2
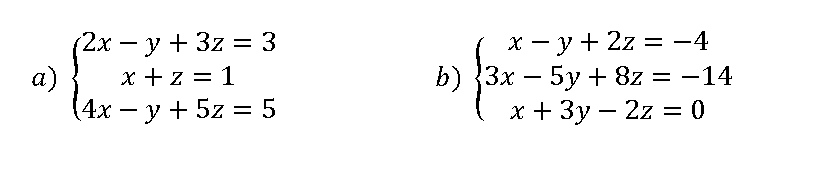
lo genial del método de Gauss es que es aplicable a sistemas con cualquier número de incógnitas , para verificarlo vamos a resolver un sistem de 4 ecuaciones con 4 incógnitas
Sistemas de 4 ecuaciones con 4 incógnitas
Igual que es los sistemas de ecuaciones 3×3 , lo primero que tenemos que hacer es obtener , el sistema equivalente reducido escalonado y luego resolver el sistema.
Lo mejor es que veamos un ejemplo resuelto paso a paso
Ejercicio resuelto sistemas 4×4 método de Gauss