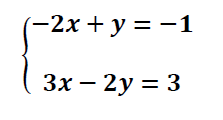Aprenderás a resolver los sistemas de ecuaciones lineales 2×2 ( dos ecuaciones con dos incógnitas) por los métodos de sustitución igualación y reducción . Vamos a resolver un ejercicio por los tres métodos que nos servirá como súper resumen de este tema
Sistemas : Métodos de sustitución igualación y reducción ejemplos con solución en vídeo
Resuelve por los tres métodos este sistema de dos ecuaciones con dos incógnitas:
Ver solución ejercicio sistemas de ecuaciones
Pasos para resolver los sistemas por el método de sustitución
Paso 1 Despejamos una incógnita ( la x o la y) en una de las ecuaciones
Paso 2 Sustituimos la incógnita despejada en la otra ecuación
Paso 3 Resolvemos la ecuación de primer grado que nos tiene que quedar
Paso 4 Sustituimos el valor obtenido en la incógnita despejada en el paso 1
Pasos para resolver los sistemas por el método de igualación
Paso 1. Despejamos una incógnita ( la x o la y) en las dos ecuaciones
Paso 2 . Igualamos las expresiones anteriores
Paso 3 Resolvemos la ecuación de primer grado que nos tiene que quedar
Paso 4 Sustituimos el valor obtenido en la incógnita despejada en el paso 1
Pasos para resolver los sistemas por el método de reducción
Este método es el menos sistemático de todos y el más “imaginativo” por eso al principio suele costar un poco más pero luego ya se le coge “cariño”
Paso 1 Multiplicamos las ecuaciones por los números pensados para obtener dos variables con el mismo coeficiente pero de distinto signo
Paso 2 Se suman las ecuaciones y nos tiene que quedar una ecuación de primer grado ( el sistema queda reducido a una ecuación )
Paso 3 Resolvemos la ecuación de primer grado con una incógnita
Paso 4 Sustituimos la incógnita calculada en una de las ecuaciones originales para obtener la otra
Qué método utilizar para resolver un sistema
Aunque depende mucho de los gustos de cada uno , en el vídeo os voy a dar una serie de CONSEJOS que probablemente os venga genial
Ver vídeo método utilizar sistemas de ecuaciones
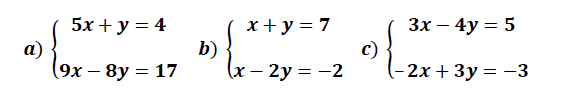
OTRAS ENTRADAS QUE TE PUEDEN INTERESAR